Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3

Extra Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

You can also download Class 10 Maths NCERT Solutions to help you to revise complete syllabus and score more marks in your examinations.

Pair of Linear Equations in Two Variables Class 10 Extra Questions Very Short Answer Type

Question 1.
Find the value of k for which the following pair of linear equations have infinitely many solutions. 2x + 3y = 7, (k + 1)x + (2k – 1 )y = 4k + 1 [CBSE 2019 Set-B]
Answer:
Given equations: 2x + 3y – 7 = 0
(k + 1)x + (2k – 1 )y – (4k + 1) = 0
Here, a₁ = 2, b₁ = 3, c₁ = – 7
a₂ = (k + 1), b₂ = (2k – 1), c₂ = – (4k + 1)
For infinitely many solutions

∴ 4k – 2 = 3k + 3
and 12k + 3 = 14k – 7
⇒ k = 5 ………………. (1)
2k = 10
⇒ k = 5 ………………. (2)
Using (1) and (2) ⇒ k = 5.

Question 2.
Find the relation between p and y if x = 3 and y = 1 is the solution of the pair of equations x – 4y + p = 0 and 2x + y – q – 2 = 0 [CBSE 2019 (C)]
Answer:
Since x = 3, y = 1 is the solution of
x – 4y + p = 0 …………….. (i)
2x + y – q – 2 = 0 …………… (ii)
So, x = 3, y = 1 must satisfy both (i) and (ii).
⇒ 3 – 4(1) + p = 0 ⇒ p = 1.
and 2(3) + (1) – q – 2 = 0 ⇒ q = 5
Since, 1 = – 4 + 5
∴ p = 1 = – 4 + 5
= q – 4
⇒ p = q – 4
Thus, p is lesser than q by 4.

Question 3.
In Fig., ABCD is a rectangle. Find the values of x and y. [CBSE 2018]

Answer:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8

Question 4.
Name the geometrical figure enclosed by graph of the equations x + 7 = 0, y – 2 = 0 and x – 2 = 0, y + 7 = 0.
Answer:
Clearly, a square of side 9 units is enclosed by lines.

Question 5.
Determine whether the following system of linear equations is inconsistent or not.
3x – 5y = 20
6x – 10y = -40
Answer:
Given
3x – 5y = 20 ……… (i)
6x – 10y = – 40 ………… (ii)

Hence given pair of linear equation are parallel.
∴ It is inconsistent.

Question 6.
If 51x + 23y = 116 and 23x + 51y = 106, then find the value of (x – y).
Answer:
51x + 23y = 116 ……….. (i)
23x + 51y = 106 ………… (ii)
Subtracting (ii) from (i)
28x – 28y = 10
28(x – y) = 10
⇒ (x – y) = \(\frac{10}{28}\) = \(\frac{5}{14}\)

Question 7.
For what value of V the point (3, a) lies on the line represented by 2x – 3y = 5?
Answer:
Since (3, a) lies on the equation 2x – 3y = 5.
∴ (3, a) must satisfy this equation
⇒ 2(3) – 3(a) = 5
⇒ 6 – 3a = 5
⇒ – 3a = 5 – 6 = – 1
a = \(\frac{1}{3}\)
∴ a = \(\frac{1}{3}\)

Pair of Linear Equations in Two Variables Class 10 Extra Questions Short Answer Type-1

Question 1.
Solve the following pair of linear equations using elimination method. [CBSE Delhi 2016]
x – y + 1 = 0; 4x + 3y – 10 = 0
Answer:
x – y + 1 = o …………. (i)
4x + 3y – 10 = 0 ……… (ii)
Eq (i) is multiplied by 4, then we get
4x – 4y + 4 = 0
By elimination method.

7y = 14
∴ y = 2
Putting y = 2 in (i), we get
x = 1
Hence, x = 1, y = 2

Question 2.
Find the values of k for which the pair of linear equations kx + y = k² and x + ky = 1 have infinitely many solutions. [CBSE Sample Paper 2017]
Answer:
We have

I^st & 2^nd Ratio ⇒ k² = 1
⇒ k = ±1 ……………. (i)
2^nd & 3^rd Ratio ⇒ k³ = 1
⇒ k = 1 ………………. (ii)
(i) and (ii) ⇒ k = 1.

Question 3.
Find out whether the following pair of equation is consistent or inconsistant.
3x + 2y = 5; 2x – 3y = 7
Answer:
Here a₁ = 3; a₂ = 2; b₁ = 2, b₂ = – 3, c₁ = 5, c₂ = 7

Hence, the equations will have a unique solution.

Question 4.
For what value of k,
2x + 2y + 2 = 0
4x + ky + 8 = 0
will have unique solution.
Answer:
Here,
a₁ = 2, b₁ = 2, c₁ = 2
a₂ = 4, b₂ = k, c₂ = 8
For the given system of linear equations to have a unique solution.
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
∴ \(\frac{2}{4} \neq \frac{2}{k}\)
⇒ 2k ≠ 2 × 4, or k ≠ 4

Pair of Linear Equations in Two Variables Class 10 Extra Questions Short Answer Type-2

Question 1.
Solve 2x + 3y = 11 and x-2 y = -12 algebraically and hence find the value of m for which y = mx + 3. [C.B.S.E. 2019]
Answer:
2x – 3y = 11 …………….. (i)
x – 2y = – 12 …………….. (ii)
(ii) ⇒ x = 2y – 12 ……. (iii)
Substitute value of x from (iii) in (i), we get
2(2y – 12) + 3y = 11
⇒ 4y – 24 + 3y = 11
⇒ 7y = 35
⇒ y = 5
Substituting value of y = 5 in equation (iii), we get
4 = 2(5) – 12 = 10 – 12 = – 2
Hence, x = – 2, y = 5 is the required solution
Now, 5 = – 2m + 3
⇒ 2m = 3 – 5
⇒ 2m = – 2
⇒ m = – 1.

Question 2.
Represent the system of linear equations 3x + y = 5 and 2x + y = 5 graphically. From the graph, find the points where the lines intersect y-axis.
Answer:
3x + y – 5 = 0, 2x + y – 5 = 0
Given system of linear equations is:
3x + y – 5 = 0 …………… (i)
2x + y – 5 = 0 ………….. (ii)
(i) ⇒ y = 5 – 3x …………. (iii)
Table of solutions for (iii)

(ii) ⇒ y = 5 – 2x …….. (iv)
Table of solutions for (iv)

Plot the points and draw the lines passing through them. We observe, the two lines intersect at the point (0, 5) which lies on y-axis. So from graph, we conclude that (0, 5) is the required point where the lines intersect y-axis.

Question 3.
Solve for x and y: [CBSE 2016]
x + 4y = 27xy ………. (i)
x + 2 y = 21xy ………… (ii)
Answer:
Dividing (i) and (ii) by xy. We get

Question 4.
A fraction becomes \(\frac{1}{3}\) when 1 is subtracted from the numerator and it becomes \(\frac{1}{4}\) when 8 is added to its denominator. Find the fraction.
Answer:
Let the fraction be \(\frac{x}{y}\).
According to given conditions
\(\frac{x-1}{y}=\frac{1}{3}\) and \(\frac{x}{y+8}=\frac{1}{4}\)
⇒ 3x – 3 = y and 4x = y + 8
⇒ 3x – y – 3 = 0
and 4x – y – 8 = 0
Subtracting (it) from (i)
⇒ – x + 5 = 0
⇒ x = 5
Put x = 5 in (i), we get
3(5) – y – 3 = 0 ⇒ y = 15
⇒ y = 12
∴ Fraction is \(\frac{5}{12}\).

Question 5.
Find the two numbers whose sum is 75 and difference is 15. [CBSE 2016]
Answer:
Let x is the first number and y be the second number.

A.T.Q.

y = 30
Putting the value of y in eq. (i), we get,
x + 30 = 75
x = 75 – 30
x = 45
∴ x = 45
∴ Hence the first number = 45 and
Second number = 30

Question 6.
In a two digit number, the ten’s digit number is three times the unit’s digit. When the number is decreased by 54, the digits are reversed. Find the number.
Answer:
Let the digit at units place = x and ten’s place = y

At condition I:
y = 3x ………… (i)
Now number obtained after reversing the digit
= 10x + y

At condition II:
10y + x – 54 = 10x + y
⇒ 9x – 9y = – 54
⇒ x – y = – 6 …………. (ii)
Put y = 3x in (ii) we get x – 3x = – 6 ⇒ x = 3
Now put x = 3 in (i), we get y = 3 × 3 = 9
∴ Number is 9 × 10 + 3 = 93

Question 7.
When the son will be as old as what his father is today their ages will add upto 126 years. When the father was as old as what his son is today, their ages added upto 38 years. Find their present ages.
Answer:
Let son’s present age be x years and father’s present age be y years.
Difference in father’s and son’s age = (y – x) years
If this difference is added to son’s age, then the son would turn as old as his father is now and at the time the father’s age will be [y + (y – x)] years. Also if we subtract this difference from father’s present age, then father would be as old as his son is today and at that time son’s age will be [x – (y – x)] years.
Thus, Condition I:
⇒ [x + (y – x)] + [y + (y – x)] = 126
⇒ 3y – x = 126
⇒ x – 3y = – 126 ……. (i)

Condition II:
⇒ [y – (y – x)] + [x – (y – x)] = 38
⇒ 3x – y = 38 …… (ii)
(i) + (ii) ⇒ 4(x – y) = – 88
⇒ x – y = – 22 ……. (iii)
(ii) – (i) ⇒ 2(x + y) = 164
⇒ x + y = 82 …….. (iv)
(iii) + (iv) ⇒ 2x = 60
⇒ x = 30
(iv) – (iii) ⇒ 2 y = 104
⇒ y = 52
Hence, present age of father is 52 years and that of son is 30 years.

Question 8.
4 chairs and 3 tables cost ₹ 2100 and 5 chairs and 2 tables cost ₹ 1750. Find the cost of one chair and one table separately. [CBSE Delhi 2016]
Answer:
Let the cost of one chair = ₹ x
and and the cost of one table = ₹ y
According to question,
4x + 3 y = 2100 ………….. (i)
5x + 2y = 1750 ………….. (ii)
[4x + 3y = 2100] × 2 ……………. (iii)
[5x + 2y = 1750] × 3 ……………. (iv)
Subtracting (iii) from (iv),
we get
7x = 1050
∴ x = 150
Putting the value of x in (i), we get
4 × 150 + 3y = 2100
∴ 3y = 2100 – 600 = 1500
∴ y = 500
∴ cost of one chair = ₹ 150
and cost of one table = ₹ 500

[Important Tips: If the present age of a person is x years, i J then, n years later his age = (x + n) years whereas m j i years ago his age = (x – m) years.]

Question 9.
A number consists of two digits. When it is divided by the sum of the digits, the quotient is 6 with no remainder. When the number is diminished by 9, the digit are reversed.
Answer:
Let the ten’s and unit’s digit of a number be ‘x’ and y respectively.
Required number = 10 × x + 1 × y = 10x + y
Reversed number = 10 × y + 1 × x = 10y + x
According to condition I, we have:
⇒ \(\frac{\text { Number }}{\text { Sum of digits }}\) = \(\frac{10 x+y}{x+y}=\frac{6}{1}\)
⇒ 10x + y = 6x + 6y
4x – 5y = 0 ……… (i)
According to condition II, we have:
⇒ Reversed number = Number – 9
⇒ 10y + x = (10x + y) – 9
⇒ 9(x – y) = 9 ⇒ x – y = 1 …….. (ii)
(i) ⇒ x = \(\frac{5}{4}\) y
Putting this value of x in (ii), we get
\(\frac{5}{4}\)y – y = 1 ⇒ \(\frac{1}{4}\)y = 1 ⇒ y = 4
Putting y = 4 in (i), we get
x = \(\frac{5}{4}\) × 4 = 5 4
∴ Required number = 54

Question 10.
Seven times a two digit number is equal to four times the number obtained by reversing the order of the digits. If the difference of the digits is 3, determine the number.
Answer:
Let Ten’s and Units digits be y and x respectively.
∴ Value of Number is 10y + x
Value of Number on reversal = 10x + y
According to as given:
7(10y + x) = 4(10x + y)
⇒ 70y + 7x = 40x + 4 y
⇒ 66y = 33x or 2y = x
Also x – y = 3 ………. (ii)
Put the value of x in (ii) form (i)
2y – y = 3 ⇒ y = 3
Put for y in (z)
x = 2(3) = 6
Hence the number is 36.

Pair of Linear Equations in Two Variables Class 10 Extra Questions Long Answer Type 1

Question 1.
Draw the graph of 2x + y = 6 and 2x – y + 2 = 0. Shade the region bounded by these lines and x-axis. Find the area of the shaded region. [CBSE 2007]
Answer:
The given system of equation is
2x + y – 6 = 0 ………. (i)
2x – y + 2 = 0 ……… (ii)
Let us write three solutions for each equation of the system in a table.
(i) ⇒ y = 6 – 2x
Table of solutions for 2x + y – 6 = 0

Similarly (ii) ⇒ y = 2x + 2

Table of solutions for 2x – y + 2 = 0

Plotting these points of each table of solutions on the same graph paper and joining them by a ruler, we obtain graph of two lines represented by equation (i) and (ii) respectively as shown in the graph below. Since, the two lines intersect at point P(1, 4). Thus x = 1, y = 4 is the solution of the given system of equations.
In graph, area bounded by the lines and x-axis is ∆PAB which is shaded.

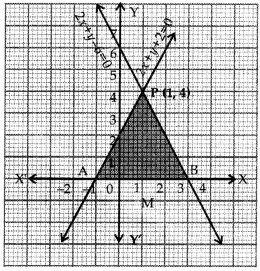
Draw PM ⊥ x-axis
Clearly, PM = y-coordinate of P(1, 4)
= 4 units
Also AB = 1 + 3 = 4 units
∴ Area of shaded region
= Area of ∆PAB = \(\frac{1}{2}\) × AB × PM
= \(\frac{1}{2}\) × 4 × 4 = 8 sq. units.

Question 2.
A man travel 370 km partly by train and partly by car. If he covers 250 km by train and the rest by car, it takes him 4 hours. But, if he travels 130 km by train and the rest by car, he takes 18 minutes longer. Find the speed of the train and that of the car. [CBSE 2001]
Answer:
Let speed of the train= x km/ hour
Speed of the car = y km/hour

Case I:
Total distance travelled = 370 km
Distance travelled by train = 250 km
Distance travelled by car = (370 – 250) km = 120 km

or 250y + 120x = 4xy
or 60x + 125y = 2xy

Case II.
Total distance covered = 370 km
Distance covered by train = 130 km
Distance covered by car = (370 -130) km = 240
Time taken by train = \(\frac{130}{x}\) hour
Time taken by car = \(\frac{240}{y}\) hour
According to 2nd condition,
\(\frac{130}{x}+\frac{240}{y}\) = 4 hour 18 minutes
\(\frac{130}{x}+\frac{240}{y}=\frac{43}{10}\)
1300y + 2400x = 43xy
or 2400x + 1300y = 43xy
Multiplying equation (i) by 40, we get

or x = 100
From (i) and (iii), we get
60(100) + 125y = 2(100)y
6000 + 125y = 200y
or (200 – 125) y = 6000
or 75y = 6000
or y = \(\frac{6000}{75}\) = 80
Hence, speed of train and car are 100 km/hour and 80 km/hour respectively.

Question 3.
Draw the graphs of the following equations:
2x – y = 1, x + 2y = 13
(i) Find the solution of the equations from the graph.
(ii) Shade the triangular region formed by lines and the y-axis.
Answer:
2x – y = 1 …………….. (i)
x + 2y = 13 ………………. (ii)
Let us draw table of values for (i) and (ii)

Plotting these points on the graph paper, we see that the two lines representing equations (i) and (ii) intersect at point (3, 5).
(i) Therefore, (3, 5) is solution of given system,
(ii) Also, that two lines enclose a triangular region (∆ABC) with y-axis which is shaded in graph.

Question 4.
The taxi charges in a city comprise of a fixed charges together with charge for the distance covered. For a journey of 10 km, the charges paid is ₹75 and for a journey of 15 km, the charges paid is ₹110. What will a person has to pay for travelling a distance of 25 km?
Answer:
Let fixed charges of taxi be ₹x and charges for covering distance be ₹y per km.
Then, according to the question, we have
x + 10y = 75 ……… (i)
and x + 15y = 110
Subtracting (i) from (ii), we get
5y = 35 ⇒ y = 35 ÷ 5 = 7
Putting y = 7 in (i), we get
x + 10 (7) = 75
⇒ x = 75 – 70 = 5
∴ Person will have to pay for travelling a distance of 25 km = x + 25y = 5 + 25(7) = ₹180.

Question 5.
Solve the following system by drawing their graph:
\(\frac{3}{2}\)x – \(\frac{5}{4}\)y = 6, 6x – 6y = 20.
Determine whether these are consistent, inconsistent or dependent.
Answer:

Plotting the points and joining by a ruler in each case. Here, we see that the graph of given equations are parallel lines. The two lines have no point in common. The given system of equations has no solution and is, therefore, inconsistent.

Pair of Linear Equations in Two Variables Class 10 Extra Questions HOTS

Question 1.
Students of a class are made to stand in rows. If one student is extra in a row, there would be 2 rows less. If one student is less in a row there would be 3 rows more. Find the number of students in the class. [CBSE 1994]
Answer:
Let the number of students in a class = x
Number of rows for students = y
Number of students in one row
= \(\frac{\text { Total no. of students }}{\text { Number of rows }}=\frac{x}{y}\)
According to 1st condition,

– 10 + y – 2 = 0
y = 12 ………… (iv)
From (iii) and (iv), we get
x = 5 × 12 = 60
Hence, number of students in class is 60.

Question 2.
If 45 is subtracted from twice the greater of two numbers, it results in the other number. If 21 is subtracted from twice the smaller number, it results in greater number. Find the numbers.
Answer:
Let x, y (x > y) be the required numbers.

First condition:
According to it:
2x – 45 = y
⇒ 2x – y – 45 = 0 …… (i)

Second condition:
According to it:
2y – 21 = x
⇒ x – 2y + 21 = 0 ……… (ii)
Multiplying (i) by 2 and subtracting from (ii), we get
(x – 2y + 21) – 2(2x – y – 45) = 0
⇒ x – 2y + 21 – 4x + 2y + 90 = 0
⇒ – 3x + 111 = 0
⇒ x = \(\frac{111}{3}\) = 37
Putting x – 37 in (i), we get
2 × 37 – 45 = y
⇒ y = 74 – 45
⇒ y = 29
∴ The required numbers are 37, 29.

Question 3.
A two digit number is a times the sum of its digits find out how many times the sum of digits equals the number formed by interchanging the digits.
Answer:
Let the digit at the unit’s place be x and the digit at the ten’s place by y.
Two digit number = 10y + x
Again, number formed by interchanging the digits = 10x + y
According to the question,
10y + x = α(x + y) ……….. (i)
and 10x + y = k(x + y) ………… (ii)
From (i), we get
(1 – α)x + (10 – α)y = 0 ………… (iii)
From (ii), we get (10 – k)x + (1 – k)y = 0 ………….. (iv)
∴ \(\frac{1-\alpha}{10-k}=\frac{10-\alpha}{1-k}\)
⇒(1 – α) (1 – k) = (10 – α) (10 – k)
⇒ 1 – k – α + αk = 100 – 10k – 10α + αk
⇒ 9k + 9α = 99
⇒ k + α = 11 ⇒ k = 11 – α
Hence, (11 – α) times sum of digits equal the number obtained by reversing the digits.

Question 4.
A cistern is supplied by three pipes, two of the pipes conveying equal volumes of water. When one of these two pipes and the third pipe are simultaneously opened, the cistern is filled in 12 minutes, but when all the three pipes are opened, the cistern is filled in 7 minutes and 30 seconds. How long does each pipe take separately to fill the cistern?
Answer:
Let each of the pipe of equal dimension takes x minutes to fill the whole cistern, and the third pipe takes y minutes.
So, any one of the two equal pipes fills in 1 minute \(\frac{1}{x}\) th of the cistern and the third pipe fills in 1 minute \(\frac{1}{y}\) th of the cistern.
∴ One of the two equal pipes and the third pipe fill in 1 minute \(\left(\frac{1}{x}+\frac{1}{y}\right)\)th of the cistern.
But, by the condition of the problem, one of the two equal pipes and the third pipe fill in 1 minute \(\frac{1}{12}\)th of the cistern. Then we must have:

⇒ x = 20, y = 30
∴ Two pipes of equal dimensions take 20 minutes while third pipe take 30 minutes.

Multiple Choice Questions

Choose the correct option out of four given in each of the following:

Question 1.
The system of equations – 3x + 4y = 5 and \(\frac{9}{2}\) – 6y + \(\frac{15}{2}\) = 0 has:
(a) Unique Solution
(b) No Solution
(c) Infinite Solution
(d) None of these
Answer:
(c) Infinite Solution

Question 2.
A pair of linear equations which have a unique solution x = 2, y = – 3 is:
(a) 2x – 3y = – 5, x + y = – 1
(b) 2x + 5y + 11 = 0, 4x + 10y + 22 = 0
(c) x – 4y – 14 = 0, 5x – y – 13 = 0
(d) 2x – y = 1, 3x + 2y = 0
Answer:
(c) x – 4y – 14 = 0, 5x – y – 13 = 0

Question 3.
If a system of pair of linear equations in two unknowns is consistent, then the lines representing the system will be
(a) parallel
(b) always coincident
(c) always intersecting
(d) intersecting or coincident
Answer:
(d) intersecting or coincident

Question 4.
The pair of equations x = 0 and y = 0 has
(a) one solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Answer:
(a) one solution

Question 5.
A pair of system of equations x = 2, y = -2; x = 3, y = – 3 when represented graphically enclose
(a) Square
(b) Trapezium
(c) Rectangle
(d) Triangle
Answer:
(c) Rectangle

Question 6.
If two lines are parallel to each other then the system of equations is
(a) consistent
(b) inconsistent
(c) consistent dependent
(d) (a) and (c) both
Answer:
(b) inconsistent

Question 7.
If lq ≠ mp, then the system of equations lx + my = c, px + qy = k
(a) has a unique solution
(b) has no solution
(c) has infinitely many solutions
(d) may or may not have a solution
Answer:
(a) has a unique solution

Question 8.
Graphically, the two systems of equations x + 7 = 0, y – 2 = 0 and x-2 = 0, j/ + 7 = 0 enclose a
(a) Square region
(b) Rectangular region
(c) triangular region
(d) Trapezium shaped region
Answer:
(a) Square region

Question 9.
If graph of two lines pass through the same points, then the system of equations representing these lines is
(a) Consistent
(b) Inconsistent
(c) Consistent dependent
(d) Inconsistent and dependent
Answer:
(c) Consistent dependent

Question 10.
If x = a, y = b is the solution of the equation x-y = 2 and x + y = 4, then the values of a and b are, respectively
(a) 3 and 5
(b) 5 and 3
(c) 3 and 1
(d) – 1 and – 3
Answer:
(c) 3 and 1

Question 11.
If the pair of equations 2x + 3y = 7 and kx + \(\frac{9}{2}\)y = 12 have no solution, then the value of k is:
(a) \(\frac{2}{3}\)
(b) \(\frac{3}{2}\)
(c) 3
(d) – 3
Answer:
(c) 3

Question 12.
₹ 2450 were divided among 65 children. If each girl gets ₹ 50 and each boy gets ₹ 30 then the number of girls are
(a) 30
(b) 40
(c) 25
(d) 27
Answer:
(c) 25

Question 13.
If 51x + 23y = 116 and 23x + 51y = 106, then value of (x – y) is
(a) \(\frac{14}{5}\)
(b) \(\frac{5}{14}\)
(c) – 5
(d) – 14
Answer:
(b) \(\frac{5}{14}\)

Question 14.
If 3x + 2y = 13 and 3x – 2y = 5, then the value of x is:
(a) 5
(b) 3
(c) 7
(d) 11
Answer:
(b) 3

Question 15.
If \(\frac{x}{2}\) + y = 0.8 and \(\) = 10,
then the value of x + y is:
(a) 1
(b) 0.6
(c) – 0.8
(d) 0.5
Answer:
(a) 1

Fill in the blanks:

Question 1.
If in a system of equation corresponding coefficients of member equations are proportional then the system has ______________ solution (s).
Answer:
Infinite

Question 2.
If in a system of equation a_1</sub1y + c₁ = 0, a₂x + b₂y + c₂ = 0, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) then the equation must ___________ at __________ point (s).
Answer:
intersect, one

Question 3.
If in a system of equations a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) then the system of equations is ____________ .
Answer:
Inconsistent

Question 4.
A pair of linear equations is said to be inconsistent if its graph lines are ____________.
Answer:
parallel

Question 5.
A pair of linear equations is said to be ____________ if its graph lines intersect or coincide.
Answer:
Consistent

Question 6.
A consistent system of equations where straight lines fall on each other is also called _____________ system of equations.
Answer:
Dependent

Question 7.
The pair of linear equations ax + by + c = 0 and lx + my + n = 0 represents two parallel lines if ____________ ____________ .
Answer:
\(\frac{a}{l}=\frac{b}{m}=\frac{c}{n}\)

Question 8.
Solution of linear equations representing 2x – y = 0, 8x + y = 25 is ____________ .
Answer:
x = 25, y = 5

Question 9.
System of linear equations representing two numbers whose ratio is 2:3 and on adding 5 to each number the ratio becomes 5 : 7 is ____________ .
Answer:
7x – 5y + 10 = 0, 3x + 2y = 0

Question 10.
The solution of √2x – √5y = 0 and √3x – √7y = 0 is ____________ .
Answer:
x = 0, y = 0

Extra Questions for Class 10 Maths

NCERT Solutions for Class 10 Maths

The post Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 appeared first on Learn CBSE.