Class 6 Maths Chapter 1 Solutions in Hindi गणित में पैटर्न

Get the simplified Ganita Prakash Class 6 Solutions and Class 6 Maths Chapter 1 Solutions in Hindi Medium गणित में पैटर्न textbook exercise question answer with complete explanation.

Ganita Prakash Class 6 Maths Chapter 1 Solutions in Hindi Medium

आइए पता लगाएँ (पृष्ठ 2)

प्रश्न 1.
क्या आप अन्य उदाहरणों के विषय में सोच सकते हैं, जहाँ गणित दैनिक जीवन में हमारी सहायता करता है?
हल:
हाँ। उदाहरणार्थ, अपने परिवार में दैनिक भोजन के लिए सब्जियों, आटा या तेल इत्यादि की मात्राओं का आकलन करना।

प्रश्न 2.
गणित ने किस प्रकार मानव को आगे बढ़ाने के लिए प्रेरित करने में सहायता की है? (आप उन उदाहरणों के विषय में विचार कर सकते हैं जिनमें वैज्ञानिक प्रयोग करना; अपनी अर्थव्यवस्था और लोकतंत्र को चलाना; पुलों, घरों या अन्य जटिल भवनों को निर्मित करना; टी.वी., मोबाइल फोन, कम्प्यूटरों, साइकिलों, रेलगाड़ियों, कारों, वायुयानों, कैलेंडरों, घड़ियों इत्यादि को बनाना सम्मिलित हैं।)
हल:
इसने मानव को आगे बढ़ाने के लिए प्रेरित करने में अनेक प्रकार से अधिक तथा और अधिक संशोधित प्रौद्योगिकी का उपयोग करके सहायता की है। उदाहरणार्थ, साइकिलों से प्रारंभ करके उच्च गुणवत्ता की कारों तक भाप के इंजनों की रेलगाड़ी से विद्युत से चलने वाली रेलगाड़ियों तक, रेडियो से उच्च गुणवत्ता वाले टेलीविजनों तक साधारण टेलीफोनों से विभिन्न प्रकार के मोबाइल फोनों तक, इत्यादि।

आइए पता लगाएँ (पृष्ठ 3)

प्रश्न 1.
क्या आप सारणी 1 में दिए प्रत्येक अनुक्रम में पैटर्न की पहचान कर सकते हैं?
हल:
हाँ।

प्रश्न 2.
सारणी 1 में दिए प्रत्येक अनुक्रम को उसकी अगली तीन संख्याओं सहित अपनी नोटबुक पर पुनः लिखिए। प्रत्येक अनुक्रम के बाद, उस अनुक्रम में संख्याओं को बनाने वाले नियम को अपने शब्दों में लिखिए।
हल:
निर्देशानुसार कीजिए।
1, 1, 1 (सभी 1);
8, 9, 10 (1 जोड़ा गया है);
15, 17, 19 (2 जोड़ा गया है);
16, 18, 20 (2 जोड़ा गया है);
36, 45, 55 (पिछली संख्याओं में 8, 9, 10 जोड़े गए हैं);
64, 81, 100 (8, 9 और 10 का वर्ग);
343, 512, 729 (7, 8, 9 के घन);
34, 55, 89 (अंतिम दो संख्याओं को जोड़ा गया है);
128, 256, 512 (संख्या को 2 से गुणा किया गया है);
2187, 6561, 19683 (संख्या को 3 से गुणा किया गया है)।

आइए पता लगाएँ (पृष्ठ 5-6)

प्रश्न 1.
सारणी 2 में दिए संख्या अनुक्रमों को चित्रात्मक रूप से दर्शाने के लिए अपनी नोटबुक में प्रतिलिपि बनाकर प्रत्येक अनुक्रम के लिए अगला चित्र बनाइए।
नोट- निर्देशानुसार कीजिए।

प्रश्न 2.
1, 3, 6, 10, 15,….. त्रिभुजाकार संख्याएँ क्यों कहलाती हैं?
1, 4, 9, 16, 25,…… वर्ग संख्याएँ या वर्ग क्यों कहलाती हैं?
1, 8, 27, 64, 125,….. घन संख्याएँ या घन क्यों कहलाती हैं?
हल:
1, 3, 6, 10, 15, …… त्रिभुजाकार संख्याएँ कहलाती हैं, क्योंकि इन्हें बिंदुओं के उपयोग से त्रिभुजों के आकार में व्यवस्थित किया जा सकता है।
1, 4, 9, 16, 25, …… वर्ग संख्याएँ कहलाती हैं, क्योंकि इन्हें बिंदुओं के उपयोग से वर्गों के आकार में व्यवस्थित किया जा सकता है।
1, 8, 27, 64, 125, ….. घन संख्याएँ कहलाती हैं, क्योंकि इन्हें बिंदुओं के उपयोग से घनों के आकार में व्यवस्थित किया जा सकता है।

प्रश्न 3.
आपने ध्यान दिया होगा कि 36 एक त्रिभुजाकार संख्या और वर्गाकार संख्या दोनों है। अर्थात् 36 बिंदुओं को त्रिभुज और वर्ग दोनों में पूरी तरह व्यवस्थित किया जा सकता है। इसे स्पष्ट करते हुए अपनी नोटबुक में चित्र बनाइए।
इससे ज्ञात होता है कि एक ही संख्या को अलग-अलग तरीकों से दर्शाया जा सकता है और संदर्भ के आधार पर अलग-अलग भूमिकाएँ निभाई जा सकती हैं। कुछ अन्य संख्याओं को अलग-अलग तरीकों से चित्रात्मक रूप से दर्शाने का प्रयास कीजिए।
हल:
निर्देशानुसार कीजिए। एक अन्य उदाहरण, 64 को वर्ग और घन संख्याओं के रूप में निरूपित कीजिए।

प्रश्न 4.
आप संख्याओं के निम्नलिखित अनुक्रम को क्या कहेंगे?

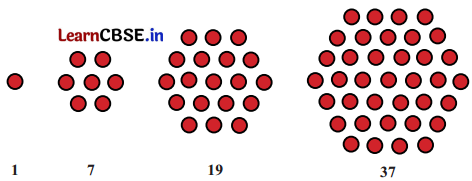
इन्हें षड्भुजाकार संख्याएँ कहते हैं। इन्हें अपनी नोटबुक में बनाइए। अनुक्रम में अगली संख्या क्या होगी?
हल:
निर्देशानुसार कीजिए।
अगली संख्या (37 + 4 × 6) = 61 है।

प्रश्न 5.
क्या आप ‘2 की घात’ के अनुक्रम का चित्रीय निरूपण कर सकते हैं? ‘3 की घात’ का?
यहाँ ‘2 की घात’ के चित्रात्मक प्रस्तुतीकरण का एक संभावित तरीका दिया है-

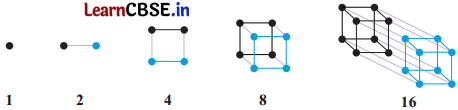
हल:
हाँ। 2 की घातों के लिए, यह पुस्तक में पहले ही स्पष्ट किया जा चुका है। 3 की घातों के लिए 2 की घातों की स्थिति की ही तरह इस अंतर के साथ 1 बिंदु से प्रारंभ कीजिए जो 1 (3⁰) निरूपित करता है, फिर तीन बराबर भागों में विभाजित एक रेखाखंड, (जो 3¹ निरूपित करता है), फिर इस रेखाखंड पर बना एक वर्ग लिया जाएगा, जो 9 बराबर भागों में विभाजित किया जाएगा (3² निरूपित करेगा), फिर इस वर्ग के आधार वाला एक घन होगा जो 27 बराबर (3³ निरूपित करेगा) भागों में विभाजित किया जाएगा, इसके बाद ऐसे 3 घनों से बना एक घनाभ होगा, जो 81 (3⁴ ) निरूपित करेगा, इसके बाद ऐसे 27 बराबर भाग वाले 9 घनों से बना एक अन्य घनाभ होगा, जो 243 (3⁵) निरूपित करेगा और आगे भी ऐसा होता रहेगा, जैसे कि नीचे दर्शाया गया है।

पृष्ठ 7

प्रश्न 1.
इसी प्रकार एक अन्य चित्र बनाकर, क्या आप यह बता सकते हैं कि प्रथम 10 विषम संख्याओं का योग क्या है?
हल:
हाँ, यह योग 100 है।

प्रश्न 2.
अब एक ऐसे ही चित्र की कल्पना कीजिए या आवश्यकतानुसार आंशिक चित्र बनाकर क्या आप बता सकते हैं कि प्रथम 100 विषम संख्याओं का योग क्या है? ऐसे चित्र की कल्पना कीजिए और आवश्यकतानुसार छोटे आकार में बनाकर इसे समझाइए।
हल:
हाँ, यह योग 10000 है।

आइए पता लगाएँ (पृष्ठ 8-9)

प्रश्न 1.
गणन संख्याओं को ऊपर और नीचे जोड़ने पर अर्थात् 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, …, से वर्ग संख्याएँ क्यों प्राप्त होती हैं, क्या आप इसके लिए एक चित्रीय स्पष्टीकरण दे सकते हैं?
हल:
ये वर्ग 1, 4, 9, 16, 25, 36 प्रदान करते हैं।

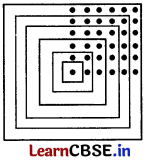
प्रश्न 2.
इस तस्वीर के बड़े संस्करण की कल्पना करके या आवश्यकतानुसार उसका आंशिक चित्र बनाकर, क्या आप ज्ञात कर सकते हैं कि 1 + 2 + 3 + ……… + 99 + 100 + 99 + …….. + 3 + 2 + 1 का मान क्या होगा?
हल:
हाँ, 100 × 100 = 10000 है।

प्रश्न 3.
जब आप सभी ‘1’ वाले अनुक्रम को ऊपर की ओर जोड़ना प्रारंभ करते हैं, तब आपको कौन-सा अनुक्रम प्राप्त होता है? जब आप सभी ‘1’ वाले अनुक्रम को ऊपर और नीचे जोड़ते हैं, तब कौन-सा अनुक्रम प्राप्त होता है?
हल:
1, 2, 3, (1, 1 + 1, 1 + 1 + 1, …),
1, 3, 5, (1, 1 + 1 + 1, 1 + 1 + 1 + 1 + 1,…) है।

प्रश्न 4.
जब आप गणन संख्याओं को ऊपर की ओर जोड़ना प्रारंभ करते हैं, तब आपको कौन-सा अनुक्रम प्राप्त होता है? क्या आप एक छोटे से चित्र के माध्यम से स्पष्टीकरण दे सकते हैं?
हल:
1, (1 + 2), (1 + 2 + 3), (1 + 2 + 3 + 4), …….. अर्थात्, 1, 3, 6, 10, ……. है।
चित्रीय निरूपण इस प्रकार है:

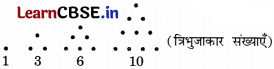
प्रश्न 5.
जब आप क्रमागत त्रिभुजाकार संख्याओं के युग्मों को जोड़ते हैं तब क्या होता है? उदाहरण के लिए, 1 + 3, 3 + 6, 6 + 10, 10 + 15, को लीजिए। आप कौन-सा अनुक्रम मिलता है? क्यों? क्या आप इसे एक चित्र द्वारा स्पष्ट कर सकते हैं?
हल:
4, 9, 16, 25, ……; वर्ग संख्याओं का अनुक्रम।
चित्रीय निरूपण :

प्रश्न 6.
जब आप 1 से प्रारंभ करते हुए 2 की घातों को जोड़ना प्रारंभ करते हैं तब क्या होता है? उदाहरण के लिए, 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, …….. लीजिए? अब, इनमें से प्रत्येक संख्या में 1 जोड़ दीजिए आप कौन-सी संख्याएँ प्राप्त करते हैं? ऐसा क्यों होता है?
हल:
हम 2, 4, 8, 16 इत्यादि प्राप्त करते हैं। ये 2 की घातें हैं। 1 को जोड़ने पर प्रथम पद 2 हो जाता है तथा अन्य पदों में सभी संख्याओं का योग (अंतिम संख्या को छोड़कर) अंतिम संख्या के बराबर हो जाता है।

प्रश्न 7.
जब आप त्रिभुजाकार संख्याओं को 6 से गुणा करते हैं और 1 जोड़ते हैं तो क्या होता है? आपको कौन-सा अनुक्रम मिलता है? क्या आप इसे चित्र के माध्यम से समझा सकते हैं?
हल:
हम अनुक्रम 7, 19, 37, 61, 91, ……. प्राप्त करते हैं। यह षड्भुजाकार संख्याओं का अनुक्रम है।

प्रश्न 8.
जब आप षड्भुजाकार संख्याओं को जोड़ना प्रारंभ करते हैं तब क्या होता है? उदाहरण के लिए, 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, …… लीजिए? आप कौन-सा अनुक्रम प्राप्त करते हैं? क्या आप इसे एक घन के चित्र का उपयोग करते हुए स्पष्ट कर सकते हैं?

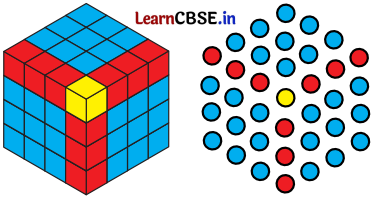
हल:
हम 1, 8, 27, 64, …….. प्राप्त करते हैं। यह घन संख्याओं का अनुक्रम है। इसे उपरोक्त घन के प्रथम चित्र के उपयोग से स्पष्ट किया जा सकता है।

प्रश्न 9.
सारणी 1 में दिए गए अनुक्रमों में और दो भिन्न अनुक्रमों के उनके बीच स्वयं अपनी ओर से अन्य पैटर्न या संबंध खोजिए। क्या एक चित्र या किसी अन्य माध्यम से आप यह स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
नोट- निर्देशानुसार कीजिए।

आइए पता लगाएँ (पृष्ठ 11)

प्रश्न 1.
क्या आप सारणी 3 के प्रत्येक अनुक्रम में पैटर्न की पहचान कर सकते हैं?
हल:
हाँ।

प्रश्न 2.
सारणी 3 के प्रत्येक अनुक्रम को अपनी नोटबुक में पुनः बनाने का प्रयास कीजिए। क्या आप प्रत्येक अनुक्रम में अगले आकार को खींच सकते हैं? क्यों और क्यों नहीं? प्रत्येक अनुक्रम के बाद, अपने शब्दों में उस नियम या पैटर्न की व्याख्या कीजिए, जिसके अनुसार उस अनुक्रम में आकार बन रहे हैं।
नोट- निर्देशानुसार कीजिए।

आइए पता लगाएँ (पृष्ठ 11-12)

प्रश्न 1.
सम बहुभुजों के प्रत्येक आकार अनुक्रम में भुजाओं की संख्या ज्ञात कीजिए। आपको कौन-सा संख्या अनुक्रम प्राप्त होता है? समबहुभुजों के प्रत्येक आकार अनुक्रम में आकृतियों के कोनों के विषय में आप क्या कहेगे? क्या आपको वही संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
हल:
भुजाओं 3, 4, 5, 6, 7, 8, 9, 10 के आकारों का अनुक्रम।

प्रश्न 2.
संपूर्ण आलेखों के प्रत्येक आकार अनुक्रम में रेखाओं की संख्याओं की गणना कीजिए। इससे आपको कौन-सा संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
हल:
भुजाओं 1, 3, 6, 10, 15, ……. (अर्थात् त्रिभुजाकार संख्याओं का) का अनुक्रम।

प्रश्न 3.
ढेरित (Stacked) वर्गों के अनुक्रम के प्रत्येक आकार में कितने छोटे वर्ग हैं? इससे कौन-सा संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
हल:
वर्ग संख्याओं 1, 4, 9, 16, 25, …… का अनुक्रम।

प्रश्न 4.
ढेरित त्रिभुजों के अनुक्रम के प्रत्येक आकार में कितने छोटे त्रिभुज हैं? इससे कौन-सा संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
(संकेत- अनुक्रम के प्रत्येक आकार में प्रत्येक पंक्ति में कितने त्रिभुज हैं?)
हल:
वर्ग संख्याओं 1, 4, 9, 16,……. का अनुक्रम।

प्रश्न 5.
कोच हिमकण (Koch snowflake) वाले अनुक्रम में, एक आकार से अगला आकार प्राप्त करने के लिए प्रत्येक रेखाखंड ‘___’ को एक ‘गति उभार (speed bump)’ __/\__ से प्रतिस्थापित करना पड़ता है। जैसे-जैसे इसे अधिक-से-अधिक बार किया जाता है, वैसे-वैसे परिवर्तन अत्यधिक छोटे-छोटे रेखाखंडों के साथ छोटे तथा और अधिक छोटे होते जाते हैं। कोच हिमकण के प्रत्येक आकार में कुल कितने रेखाखंड हैं? इनके संगत संख्या अनुक्रम क्या हैं? (3, 12, 48, 192, …… है। अर्थात 4 की घात का तीन गुना इसका उत्तर हैं, यह अनुक्रम सारणी में नहीं है।)
हल:
अनुक्रम 3, 12, 48, 192, … है। अर्थात्, यह 3 × 1, 3 × 4, 3 × 16, 3 × 64, …. है। दूसरे शब्दों में, यह 3 × 4⁰, 3 × 4¹, 3 × 4², 3 × 4³, …… का अनुक्रम है अर्थात् 4 की घातों का तीन गुना वाला अनुक्रम है।

The post Class 6 Maths Chapter 1 Solutions in Hindi गणित में पैटर्न appeared first on Learn CBSE.