संघर्ष के कराण मैं तुनुकमिजाज हो गया धनराज – CBSE Notes for Class 7 Hindi
CBSE NotesCBSE Notes Class 7 HindiNCERT Solutions Hindi



The post संघर्ष के कराण मैं तुनुकमिजाज हो गया धनराज – CBSE Notes for Class 7 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 7 HindiNCERT Solutions Hindi



The post संघर्ष के कराण मैं तुनुकमिजाज हो गया धनराज – CBSE Notes for Class 7 Hindi appeared first on Learn CBSE.
NCERT Exemplar Class 11 Maths Chapter 1 Sets are part of NCERT Exemplar Class 11 Maths. Here we have given NCERT Exemplar Class 11 Maths Chapter 1 Sets.
Short Answer Type Questions
Q1. Write the following sets in the roaster from


Q2. Write the following sets in the roaster form:



Q3. If Y = {x\x is a positive factor of the number 2P(2P – 1), where 2P – 1 is a prime number}. Write Y in the roaster form.
Sol: Y- {x | x is a positive factor of the number 2P-1 (2P – 1), where 2P – 1 is a prime number}.
So, the factors of 2P-1 are 1,2,22,23,…, 2P- 1.
Y= {1,2,22,23, …,2p-1,2p-1}
Q4. State which of the following statements are true and which are false. Justify your answer.
(i) 35 ∈ {x | x has exactly four positive factors}.
(ii) 128 e {y | the sum of all the positive factorsofy is 2y}
(iii) 3∉{x|x4-5x3 + 2jc2-112x + 6 = 0}
(iv) 496 ∉{y | the sum of all the positive factors of y is 2y}.
Sol: (i) The factors of 35 are 1, 5, 7 and 35. So, 35 is an element of the set. Hence, statement is true.
(ii) The factors of 128 hre 1,2,4, 8, 16, 32, 64 and 128.
Sum of factors = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255 * 2 x 128 Hence, statement is false.
(iii) We have, x4 – 5x3 + 2x2 – 1 12jc + 6 = 0 Forx = 3, we have
(3)4 – 5(3)3 + 2(3)2 – 112(3) + 6 = 0
=> 81 – 135 + 18-336 + 6 = 0
=> -346 = 0, which is not true.
So 3 is not an element of the set
Hence, statement is true.
(iv) 496 = 24 x 31
So, the factors of 496 are 1,2,4, 8, 16,31,62, 124,248 and 496.
Sum of factors = 1 +2 + 4 + 8+ 16 + 31+62+124 + 248 + 496 = 992 = 2(496)
So, 496 is the element of the set Hence, statement is false
Q5. Given L, = {1,2, 3,4},M= {3,4, 5, 6} and N= {1,3,5}
Verify that L-(M⋃N) = (L-M)⋂(L-N)
Sol: Given L,= {1,2, 3,4}, M= {3,4,5,6} and N= {1,3,5}
M⋃N= {1,3,4, 5,6}
L – (M⋃N) = {2}
Now, L-M= {1, 2} and L-N= {2,4}
{L-M) ⋂{L-N)= {2}
Hence, L-{M⋃N) = {L-M) ⋂ (L-N).
Q6. If A and B are subsets of the universal set U, then show that
(i) A⊂ A∪ B
(ii) A⊂B⟺A∪B = B
(iii) (A∩B)⊂ A



Q7. Given that N= {1,2,3, …, 100}. Then write
(i) the subset of N whose elements are even numbers.
(ii) the subset of N whose element are perfect square numbers.
Sol: We have, N= {1,2, 3,4,…, 100}
(i) subset of N whose elements are even numbers = {2,4, 6, 8,…, 100}
(ii) subset of N whose elements are perfect square = {1,4, 9, 16, 25, 36,49, 64, 81, 100}
Q8. If X= {1, 2, 3}, if n represents any member of X, write the following sets containing all numbers represented by
(i) 4n
(ii) n + 6
(iii) n/2
(iv) n-1

Q9.If Y= {1,2,3,…, 10}, and a represents any element of Y, write the following sets, containing all the elements satisfying the given conditions.

Q10. A, B and C are subsets of Universal Set If A = {2, 4, 6, 8, 12, 20}, B= {3,6,9,12,15}, C= {5,10,15,20} and U is the set of all whole numbers, draw a Venn diagram showing the relation of U, A, B and C.

Q11. Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming. Draw a Venn diagram showing one of the possible interrelationship among sets U, G, B and S.

Q12. For all sets A, B and C, show that (A – B) ∩ (C – B) = A – (B ∪ C)


Instruction for Exercises 13-17: Determine whether each of the statements in these exercises is true or false. Justify your answer.
Q13. For all sets A and B, (A – B)∪ (A∩ B) = A
Sol: True
L.H.S. = (A-B) ∪ (A∩B) = [(A-B) ∪A] ∩ [(A – B) ∪B]
= A∩ (A-B) = A= R.H.S.
Hence, given statement is true.
Q14. For all sets A, B and C, A – (B-C) = (A- B)-C
Sol: False

Q15. For all sets A, B and C, if A ⊂ B, then A ∩C<⊂B ∩C
Sol: True
Let x ∈A∩C
=> x ∈ A and x∈ C

Q16. For all sets A, B and C, if A⊂ B, then A ∪ C⊂ B ∪ C
Sol: True

Q17. For all sets A, B and C, if A⊂ C and B ⊂ C,then A∪ B ⊂ C

Instruction for Exercises 18-22: Using properties of sets prove the statements given in these exercises.
Q18. For all sets A and B, A ∪ (B -A) = A ∪ B

Q19. For all sets A and B, A – (A – B) = A ∩ B

Q20. For all sets A and B, A – (A ∩ B) = A – B


Q21. For all sets A and B,(A ∪ B)- B = A-B


Long Answer Type Questions
Q23. Let A, B and C be sets. Then show that A ∩ (B ∪ C) = (A ∩ B)∪ (A ∩ C).

From (i) and (ii), we get . .
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Q24. Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science,6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science
(ii) in Mathematics and Science but not in English
(iii) in Mathematics only
(iv) in more than one subject only
Sol. Let M be the set of students who passed in Mathematics, E be the set of students who passed in English and S be the set of students who passed in Science.
Given n (U) = 100,
n(E) = 15, n(M) = 12, n(S) = 8,
n(E ∩ M) = 6, n(M ∩S) = 7, n(E ∩ S) — 4, and n(E ∩M ∩ S) = 4,

Number of students passed in English and Mathematics but not in Science = b = 2
(ii) Number of students passed in Mathematics and Science but not in English = d = 3
(iii) Number of students passed in Mathematics only = e = 3
(iv) Number of students passed in more than one subject = a + b + c + d =4+2+0+3=9
Q25. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither.
Sol: Let C be the set of students who play cricket and T be the set of students who play tennis.
n(U) = 60, n(C) = 25, n(T) = 20, and n(C ∩ T) = 10
n(C ∪ T) = n(C) + n(T) – n(C n T) = 25 + 20 – 10 = 35
Q26. In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
Sol: Let M be the set of students who study Mathematics, P be the set of students who study E Physics and C be the set of students who study Chemistry

Q27. In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers. Find
(a) The number of families which buy newspaper A only.
(b) The number of families which buy none of A, B and C.
Sol: Let A be the set of families which buy newspaper A, B be the set of families which buy newspaper B and C be the set of families which buy newspaper C. The

Number of families which buy none of A, B and C = 10000 x (40/100)
Q28. In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15, French and English = 09, English and Sanskrit = 4,French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
(i) French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages but not French
Sol: Let F be the set of students who study French, E be the set of students who study English and S be the set of students who study Sanskrit.
Then, n{U) = 50, n(F) =17, n{E) = 13, and n{S) = 15,
n(F ∩ E) = 9, n(E ∩ S) = 4, n(F ∩ S) = 5, n(F ∩ E ∩ S) = 3


(i) Number of students studying French only = e = 6
(ii) Number of students studying English only = g = 3
(iii) Number of students studying Sanskrit only =f= 9
(iv) Number of students studying English and Sanskrit but not French = c = 1
(v) Number of students studying French and Sanskrit but not English = d = 2
(vi) Number of students studying French and English but not Sanskrit = b = 6
(vii) Number of students studying at least one of the three languages = a + b + c + d + e+f+g = 30
(viii) Number of students studying none of the three languages but not French = 50-30 = 20


Q30. Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively, (a) 4,7 (b) 7,4 (c) 4,4 (d) 7, 7


Q32. Let F1 be the set of parallelograms, F2 the set of rectangles, F3 the set of rhombuses, F4 the set of squares and F5 the set of trapeziums in a plane. Then F1may be equal to
(a) F2 ∩F3
(b) F3 ∩F4
(c) F2 u Fs
(d) F2 ∪ F3 ∪ F4 ∪ F1
Sol: (d) Every rectangle, rhombus, square in a plane is a parallelogram but every trapezium is not a parallelogram.
F1 = F2 ∪ F3 ∪ F4 ∪ F1
Q33. Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square, then

Q34. Let R be set of points inside a rectangle of sides a and b (a, b> 1) with two sides along the positive direction of x-axis andy-axis. Then

Q35. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is
(a) 0 (b) 25 (c) 35 (d) 45
Sol: Let C be the set of students who play cricket and T be the set of students who play tennis.
n(U) = 60, n(C) = 25, n(T) = 20, and n(C ∩ T) = 10
n(C ∪ T) = n(C) + n(T) – n(C n T) = 25 + 20 – 10 = 35
Q36. In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is
(a) 210 (b) 290 (c) 180 (d) 260
Sol: (b) Let H be the set of persons who read Hindi and E be the set of persons who read English.


NCERT Exemplar ProblemsMathsPhysicsChemistryBiology
We hope the NCERT Exemplar Class 11 Maths Chapter 1 Sets help you. If you have any query regarding NCERT Exemplar Class 11 Maths Chapter 1 Sets, drop a comment below and we will get back to you at the earliest.
The post NCERT Exemplar Class 11 Maths Chapter 1 Sets appeared first on Learn CBSE.
NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions are part of NCERT Exemplar Class 11 Maths. Here we have given NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions.
Short Answer Type Questions
Q1. If A = {-1, 2, 3 } and B = {1, 3}, then determine
(i) AxB (ii) BxC (c) BxB (iv) AxA
Sol: We have A = {-1,2,3} and B = {1,3}
(i) A x B = {(-1, 1), (-1, 3), (2, 1), (2, 3), (3,1), (3, 3)}
(ii) BxA = {( 1, -1), (1, 2), (1,3), (3,-1), (3,2), (3, 3)}
(iii) BxB= {(1,1), (1,3), (3,1), (3, 3)}
(iv) A xA = {(-1, -1), (-1, 2), (-1, 3), (2, -1), (2, 2), (2, 3), (3, -1), (3, 2), (3,3)}
Q2. If P = {x : x < 3, x e N}, Q= {x : x≤2,x ∈ W}. Find (P∪ Q) x (P∩ Q), where W is the set of whole numbers.
Sol: We have, P={x: x<3,x ∈ N} = {1,2}
And Q = {x :x≤ 2,x∈ W] = {0,1,2}
P∪Q= {0, 1,2} and P ∩ Q= {1,2}
(P ∪ Q) x (P ∩ Q) = {0,1, 2} x {1,2}
= {(0,1), (0, 2), (1,1), (1,2), (2,1), (2, 2)}
Q3. lfA={x:x∈ W,x < 2}, 5 = {x : x∈N, 1 <.x < 5}, C= {3, 5}. Find
(i) Ax(B∩Q) (ii) Ax(B∪C)
Sol: We have, A = {x :x∈ W,x< 2} = {0, 1};
B = {x : x ∈ N, 1 <x< 5} = {2, 3,4}; and C= {3, 5}
(i) B∩ C = {3}
A x (B ∩ C) = {0, 1} x {3} = {(0, 3), (1, 3)}
(ii) (B ∪ C) ={2,3,4, 5}
A x (B ∪ C) = {0, 1} x {2, 3,4, 5}
= {(0,2), (0,3), (0,4), (0,5), (1,2), (1,3), (1,4), (1, 5)}
Q4. In each of the following cases, find a and b. (2a + b, a – b) = (8, 3) (ii) {a/4, a – 2b) = (0, 6 + b)
Sol: (i) We have, (2a + b,a-b) = (8,3)
=> 2a + b = 8 and a – b = 3
On solving, we get a = 11/3 and b = 2/3

Q5. Given A = {1,2,3,4, 5}, S= {(x,y) :x∈ A,y∈ A}.Find the ordered pairs which satisfy the conditions given below
x+y = 5 (ii) x+y<5 (iii) x+y>8
Sol: We have, A = {1,2, 3,4, 5}, S= {(x,y) : x ∈ A,y∈ A}
(i) The set of ordered pairs satisfying x + y= 5 is {(1,4), (2,3), (3,2), (4,1)}
(ii) The set of ordered pairs satisfying x+y < 5 is {(1,1), (1,2), (1,3), (2, 1), (2,2), (3,1)}
(iii) The set of ordered pairs satisfying x +y > 8 is {(4, 5), (5,4), (5, 5)}.
Q6. Given R = {(x,y) : x,y ∈ W, x2 + y2 = 25}. Find the domain and range of R
Sol: We have, R = {(x,y):x,y∈ W, x2 + y2 = 25}
= {(0,5), (3,4), (4, 3), (5,0)}
Domain of R = Set of first element of ordered pairs in R = {0,3,4, 5}
Range of R = Set of second element of ordered pairs in R = {5,4, 3, 0}
Q7. If R1 = {(x, y)| y = 2x + 7, where x∈ R and -5 ≤ x ≤ 5} is a relation. Then find the domain and range of R1.
Sol: We have, R1 = {(x, y)|y = 2x + 7, where x∈ R and -5 ≤x ≤ 5}
Domain of R1 = {-5 ≤ x ≤ 5, x ∈ R} = [-5, 5]
x ∈ [-5, 5]
=> 2x ∈ [-10,10]
=>2x + 7∈ [-3, 17]
Range is [-3, 17]
Q8. If R2 = {(x, y) | x and y are integers and x2 +y2 = 64} is a relation. Then find R2
Sol: We have, R2 = {(x, y) | x and y are integers and x2 + y2 – 64}
Clearly, x2 = 0 and y2 = 64 or x2 = 64 andy2 = 0
x = 0 and y = ±8
or x = ±8 and y = 0
R2 = {(0, 8), (0, -8), (8,0), (-8,0)}
Q9. If R3 = {(x, |x|) | x is a real number} is a relation. Then find domain and range
Sol: We have, R3 = {(x, |x)) | x is real number}
Clearly, domain of R3 = R
Now, x ∈ R and |x| ≥ 0 .
Range of R3 is [0,∞)
Q10. Is the given relation a function? Give reasons for your answer.
(i) h={(4,6), (3,9), (-11,6), (3,11)}
(ii) f = {(x, x) | x is a real number}
(iii) g = {(n, 1 In)| nis a positive integer}
(iv) s= {(n, n2) | n is a positive integer}
(v) t= {(x, 3) | x is a real number}
Sol: (i) We have, h = {(4,6),(3,9), (-11,6), (3,11)}.
Since pre-image 3 has two images 9 and 11, it is not a function.
(ii) We have, f = {(x, x) | x is a real number}
Since every element in the domain has unique image, it is a function.
(iii) We have, g= {(n, 1/n) | nis a positive integer}
For n, it is a positive integer and 1/n is unique and distinct. Therefore,every element in the domain has unique image. So, it is a function.
(iii) We have, s = {(n, n2) | n is a positive integer}
Since the square of any positive integer is unique, every element in the domain has unique image. Hence, ibis a function.
(iv) We have, t = {(x, 3)| x is a real number}.
Since every element in the domain has the image 3, it is a constant function.
Q11. If f and g are real functions defined byf( x) = x2 + 7 and g(x) = 3x + 5, find each of the following



Q12. Let f and g be real functions defined by f(x) = 2x+ 1 and g(x) = 4x – 7.
(i) For what real numbers x,f(x)= g(x)?
(ii) For what real numbers x,f (x) < g(x)?
Sol: We have,f(x) = 2x + 1 and g(x) = 4x-7
(i) Now f (x) = g(x)
=> 2x+l=4x-7
=> 2x = 8 =>x = 4
(ii) f (x) < g(x)
=> 2x + 1 < 4x – 7
=> 8 < 2x
=> x > 4
Q13. If f and g are two real valued ftmctions defined as f(x) = 2x + 1, g(x) = x2 + 1, then find.


Q14. Express the following functions as set of ordered pairs and determine their range.
f:X->R,f{x) = x3 + 1, where X= {-1,0, 3, 9, 7}
Sol: We have, f:X→ R,flx) = x3 + 1.
Where X = {-1, 0, 3, 9, 7}
Now f (-l) = (-l)3+1 =-l + 1 =0
f(0) = (0)3+l=0+l = l
f(3) = (3)3 + 1 = 27 + 1 = 28
f(9) = (9)3 + 1 = 729 + 1 = 730
f(7) = (7)3 + 1 = 343 + 1 = 344
f= {(-1, 0), (0, 1), (3, 28), (9, 730), (7, 344)}
Range of f= {0, 1, 28, 730, 344}
Q15. Find the values of x for which the functions f(x) = 3x2 -1 and g(x) = 3+ x are equal.
Sol: f(x) = g(x)
=> 3x2-l=3+x => 3x2-x-4 = 0 => (3x – 4)(x+ 1) – 0
x= -1,4/3
Q16. Is g = {(1, 1), (2, 3), (3, 5), (4, 7)} a function? Justify. If this is described by the relation, g(x) = x +, then what values should be assigned to and ?
Sol:We have, g = {(1, 1), (2, 3), (3, 5), (4,7)}
Since, every element has unique image under g. So, g is a function.
Now, g(x) = x + For (1,1), g(l) = a(l) + P
=> l = + (i)
For (2, 3), g(2) = (2) +
=> 3 = 2 + (ii)
On solving Eqs. (i) and (ii), we get = 2, = -l
f(x) = 2x-1
Also, (3, 5) and (4, 7) satisfy the above function.
Q17. Find the domain of each of the following functions given by




Q18. Find the range of the following functions given by



Q19. Redefine the function f(x) = |x-2| + |2+x| , -3 ≤x ≤3


Q21. Let f (x) = √x and g(x) = xbe two functions defined in the domain R+ ∪ {0}. Find
(i) (f+g)(x)
(ii) (f-g)(x)
(iii) (fg)(x)
(iv) f/g(x)


Q23. If f( x)= y = ax-b/ cx-a then prove that f (y) = x

Objective Type Questions
Q24. Let n(A) = m, and n(B) = n. Then the total number of non-empty relations that can be defined from A to B is
(a) mn
(b) nm– 1
(c) mn – 1
(d) 2mn– 1
Sol: (d) We have, n(A) = m and n(B) = n
n(A xB) = n(A). n(B) = mn
Total number of relation from A to B = Number of subsets of AxB = 2mn
So, total number of non-empty relations = 2mn – 1
Q25. If [x]2 – 5[x] + 6 = 0, where [. ] denote the greatest integer function, then
(a) x ∈ [3,4]
(b) x∈ (2, 3]
(c) x∈ [2, 3]
(d) x ∈ [2, 4)
Sol: (d) We have [x]2 – 5[x] + 6 = 0 => [(x – 3)([x] – 2) = 0
=> [x] = 2,3 .
For [x] = 2, x ∈ [2, 3)
For [x] = 3, x ∈ [3,4)
x ∈ [2, 3) u [3,4)
Or x ∈ [2,4)





Q29. If fx) ax+ b, where a and b are integers,f(-1) = -5 and f(3) – 3, then a and b are equal to
(a) a = -3, b =-1
(b) a = 2, b =-3
(c) a = 0, b = 2
(d) a = 2, b = 3







Fill in the Blanks Type Questions
Q36. Let f and g be two real functions given by f= {(0, 1), (2,0), (3,.-4), (4,2), (5, 1)}
g= {(1,0), (2,2), (3,-1), (4,4), (5, 3)} then the domain of f x g is given by________ .
Sol: We have, f = {(0, 1), (2, 0), (3, -4), (4, 2), (5,1)} and g= {(1, 0), (2, 2), (3, 1), (4,4), (5, 3)}
Domain of f = {0,2, 3, 4, 5}
And Domain of g= {1, 2, 3,4, 5}
Domain of (f x g) = (Domain of f) ∩ (Domain of g) = {2, 3,4, 5}
Matching Column Type Questions
Q37. Let f= {(2,4), (5,6), (8, -1), (10, -3)} andg = {(2, 5), (7,1), (8,4), (10,13), (11, 5)} be two real functions. Then match the following:



True/False Type Questions
Q38. The ordered pair (5,2) belongs to the relation R ={(x,y): y = x – 5, x,y∈Z}
Sol: False
We have, R = {(x, y): y = x – 5, x, y ∈ Z}
When x = 5, then y = 5-5=0 Hence, (5, 2) does not belong to R.
Q39. If P = {1, 2}, then P x P x P = {(1, 1,1), (2,2, 2), (1, 2,2), (2,1, 1)}
Sol:False
We have, P = {1, 2} and n(P) = 2
n(P xPxP) = n(P) x n(P) x n(P) = 2 x 2 x 2
= 8 But given P x P x P has 4 elements.
Q40. If A= {1,2, 3}, 5= {3,4} and C= {4, 5, 6}, then (A x B) ∪ (A x C) = {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3,4), (3, 5), (3,6)}.
Sol: True
We have.4 = {1,2, 3}, 5= {3,4} andC= {4,5,6}
AxB= {(1, 3), (1,4), (2, 3), (2,4), (3, 3), (3,4)}
And A x C = {(1,4), (1, 5), (1, 6), (2,4), (2, 5), (2, 6), (3,4), (3, 5), (3, 6)}
(A x B)∪(A xC)= {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3,3), (3,4), (3, 5), (3,6)}

Q42. If Ax B= {(a, x), (a, y), (b, x), (b, y)}, thenM = {a, b},B= {x, y}.
Sol: True
We have, AxB= {{a, x), {a, y), (b, x), {b, y)}
A = Set of first element of ordered pairs in A x B = {a, b}
B = Set of second element of ordered pairs in A x B = {x, y}
NCERT Exemplar ProblemsMathsPhysicsChemistryBiology
We hope the NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions help you. If you have any query regarding NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions, drop a comment below and we will get back to you at the earliest.
The post NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post वह चिड़िया जो – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post अक्षरों का महत्व – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi




The post नादान दोस्त – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post बचपन – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi


The post चाँद से थोड़ी सी गप्पे – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post साथी हाथ बढ़ाना – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post टिकट अलबम – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi








The post झाँसी की रानी – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post ऐसे ऐसे – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi





The post पार नज़र के – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi




The post नौकर – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post लोकगीत – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post संसार पुस्तक है – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post मैं सबसे छोटी होऊं – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
CBSE NotesCBSE Notes Class 6 HindiNCERT Solutions Hindi



The post जो देखकर भी नहीं देखते – CBSE Notes for Class 6 Hindi appeared first on Learn CBSE.
NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations are part of NCERT Exemplar Class 11 Maths. Here we have given NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations.
Short Answer Type Questions

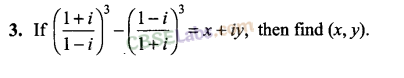
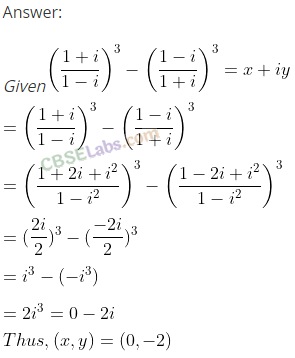
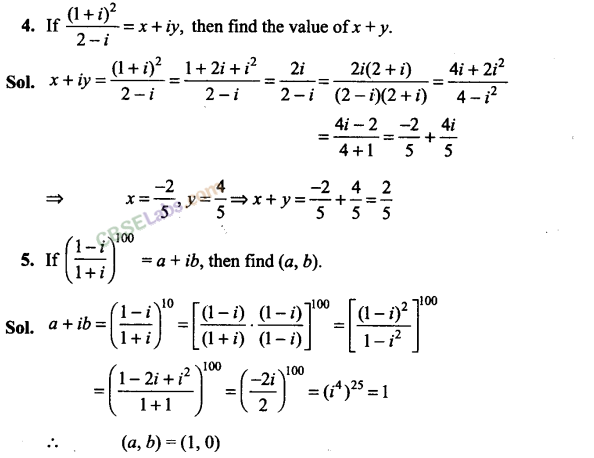
Q6. If a = cos θ + i sin θ, then find the value of (1+a/1-a)
Sol: a = cos θ + i sin θ
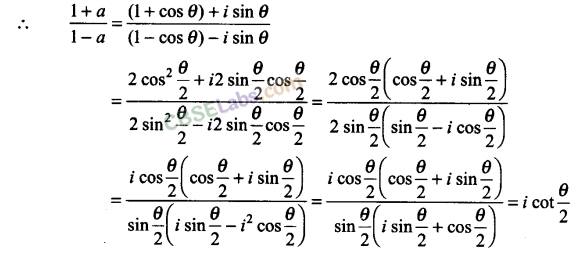

Q10. Show that the complex number z, satisfying the condition arg lies on arg (z-1/z+1) = π/4 lies on a circle.
Sol: Let z = x + iy
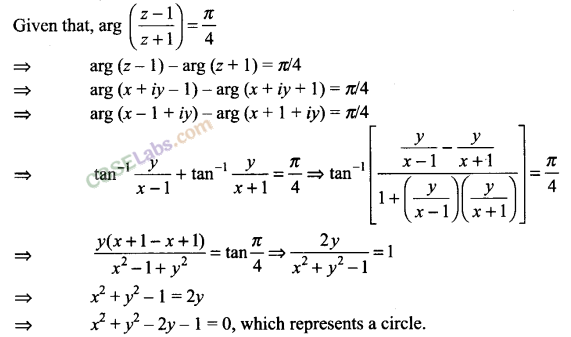
Q11. Solve the equation |z| = z + 1 + 2i.
Sol: We have |z| = z + 1 + 2i
Putting z = x + iy, we get
|x + iy| = x + iy + 1+2i
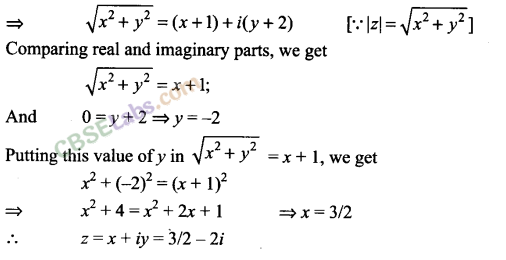
Long Answer Type Questions
Q12. If |z + 1| = z + 2( 1 + i), then find the value of z.
Sol: We have |z + 11 = z + 2(1+ i)
Putting z = x + iy, we get
Then, |x + iy + 11 = x + iy + 2(1 + i)
⟹|x + iy + l|=x + iy + 2(1 +i)
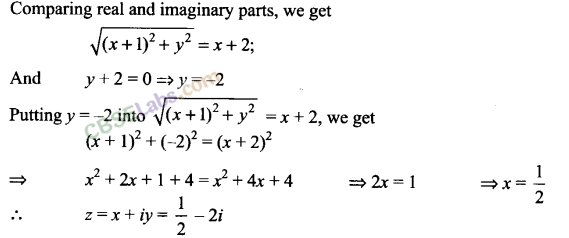
Q13. If arg (z – 1) = arg (z + 3i), then find (x – 1) : y, where z = x + iy.
Sol: We have arg (z – 1) = arg (z + 3i), where z = x + iy
=> arg (x + iy – 1) = arg (x + iy + 3i)
=> arg (x – 1 + iy) = arg [x + i(y + 3)]
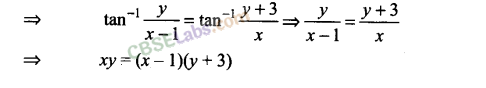
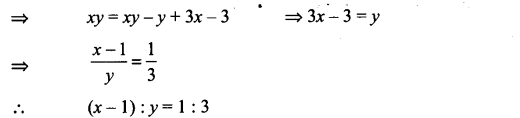
Q14. Show that | z-2/z-3| = 2 represents a circle . Find its center and radius .
Sol: We have | z-2/z-3| = 2
Puttingz=x + iy, we get
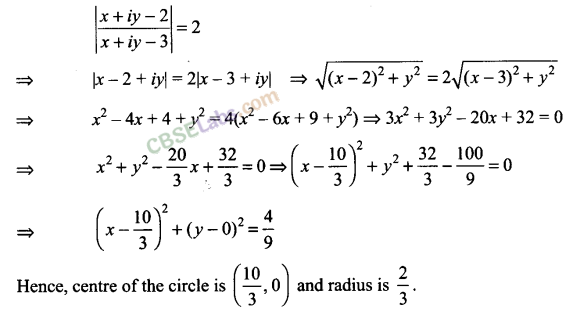
Q15. If z-1/z+1 is a purely imaginary number (z ≠1), then find the value of |z|.
Sol: Let z = x + iy
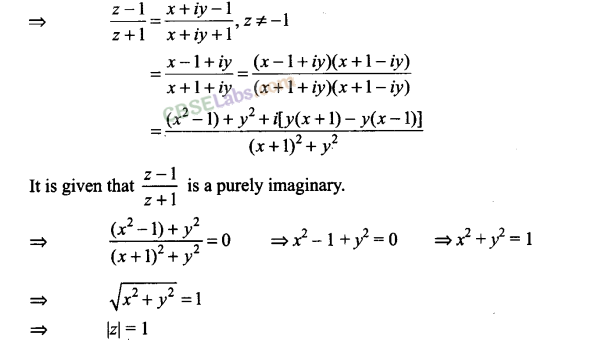
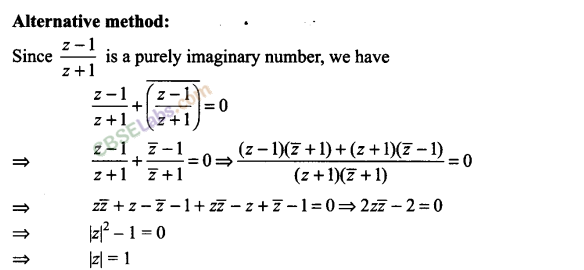

Q17. If |z1 | = 1 (z1≠ -1) and z2 = z1 – 1/ z1 + 1 , then show that real part of z2 is zero .

Q18. If Z1, Z2 and Z3, Z4 are two pairs of conjugate complex numbers, then find arg (Z1/ Z4) + arg (Z2/ Z3)
Sol. It is given that z1 and z2 are conjugate complex numbers.

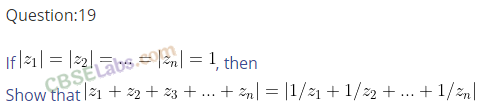
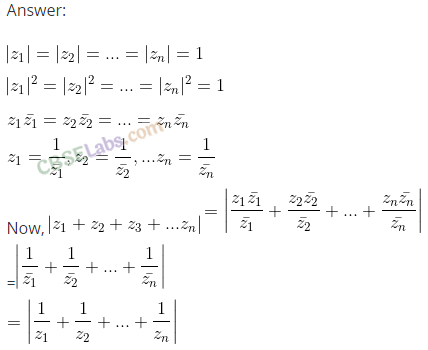
Q20. If for complex number z1 and z2, arg (z1) – arg (z2) = 0, then show that |z1 – z2| = | z1|- |z2 |
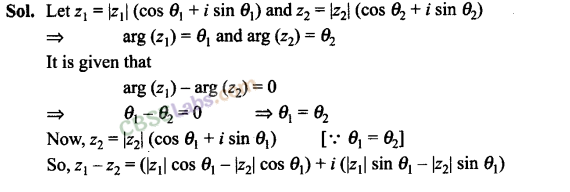

Q21. Solve the system of equations Re (z2) = 0, |z| = 2.
Sol: Given that, Re(z2) = 0, |z| = 2
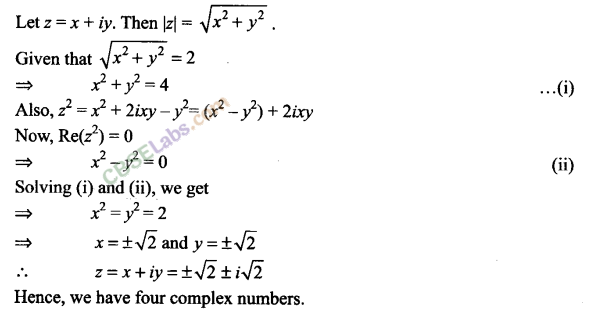
Q22. Find the complex number satisfying the equation z + √2 |(z + 1)| + i = 0.
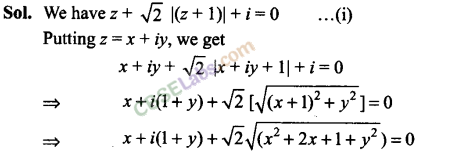
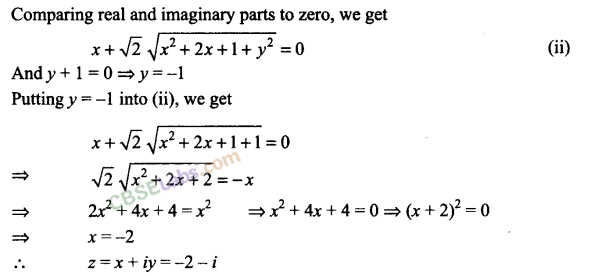

Fill in the blanks



True/False Type Questions
Q26. State true or false for the following.
(i) The order relation is defined on the set of complex numbers.
(ii) Multiplication of a non-zero complex number by -i rotates the point about origin through a right angle in the anti-clockwise direction.
(iii) For any complex number z, the minimum value of |z| + |z – 11 is 1.
(iv) The locus represented by |z — 11= |z — i| is a line perpendicular to the join of the points (1,0) and (0, 1).
(v) If z is a complex number such that z ≠ 0 and Re(z) = 0, then Im (z2) = 0.
(vi) The inequality |z – 4| < |z – 2| represents the region given by x > 3.
(vii) Let Z1 and Z2 be two complex numbers such that |z, + z2| = |z1 j + |z2|, then arg (z1 – z2) = 0.
(viii) 2 is not a complex number.
Sol:(i) False
We can compare two complex numbers when they are purely real. Otherwise comparison of complex numbers is not possible or has no meaning.
(ii) False


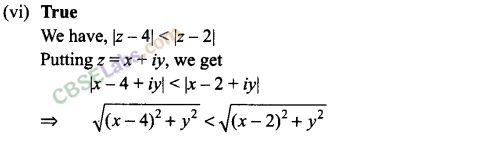

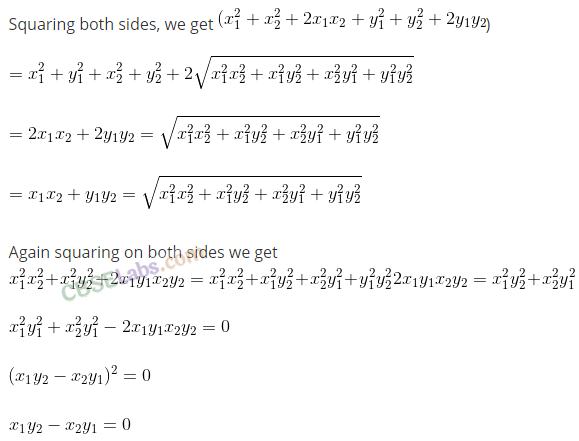

Matching Column Type Questions
Q24. Match the statements of Column A and Column B.
| Column A | Column B | ||
| (a) | The polar form of i + √3 is | (i) | Perpendicular bisector of segment joining (-2, 0) and (2,0) |
| (b) | The amplitude of- 1 + √-3 is | (ii) | On or outside the circle having centre at (0, -4) and radius 3. |
| (c) | It |z + 2| = |z – 2|, then locus of z is | (iii) | 2/3 |
| (d) | It |z + 2i| = |z – 2i|, then locus of z is | (iv) | Perpendicular bisector of segment joining (0, -2) and (0,2) |
| (e) | Region represented by |z + 4i| ≥ 3 is | (v) | 2(cos /6 +I sin /6) |
| (0 | Region represented by |z + 4| ≤ 3 is | (Vi) | On or inside the circle having centre (-4,0) and radius 3 units. |
| (g) | Conjugate of 1+2i/1-I lies in | (vii) | First quadrant |
| (h) | Reciprocal of 1 – i lies in | (viii) | Third quadrant |



Q28. What is the conjugate of 2-i / (1 – 2i)2
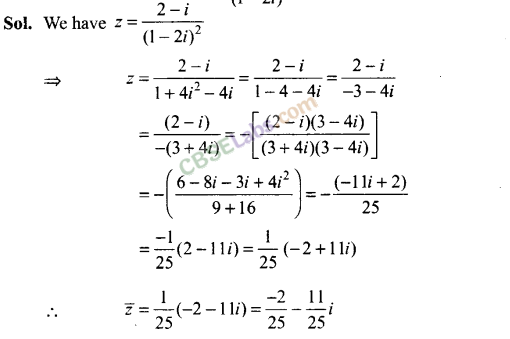
Q29. If |Z1| = |Z2|, is it necessary that Z1 = Z2?
Sol: If |Z1| = |Z2| then z1 and z2 are at the same distance from origin.
But if arg(Z1) ≠arg(z2), then z1 and z2 are different.
So, if (z1| = |z2|, then it is not necessary that z1 = z2.
Consider Z1 = 3 + 4i and Z2 = 4 + 3i
Q30.If (a2+1)2 / 2a –i = x + iy, then what is the value of x2 + y2?
Sol: (a2+1)2 / 2a –i = x + iy

Q31. Find the value of z, if |z| = 4 and arg (z) = 5π/6
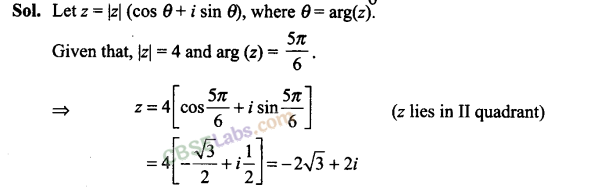




Q34. Where does z lies, if | z – 5i / z + 5i | = 1?
Sol: We have | z – 5i / z + 5i |

Instruction for Exercises 35-40: Choose the correct answer from the given four options indicated against each of the Exercises.
Q35. sin x + i cos 2x and cos x – i sin 2x are conjugate to each other for
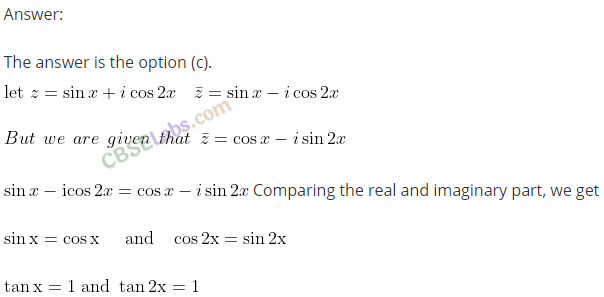

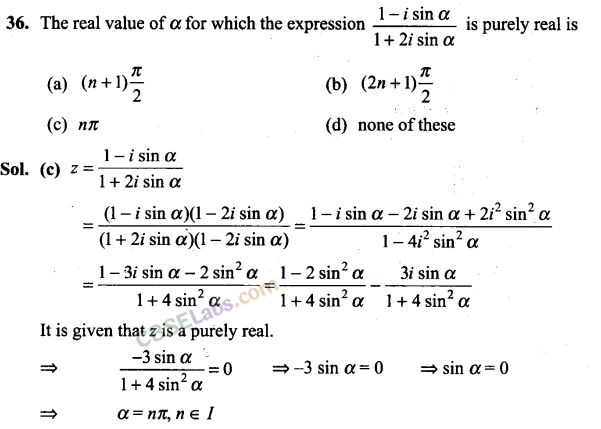

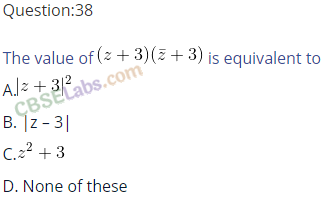
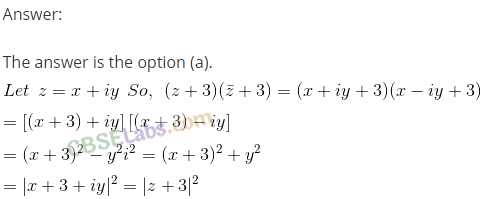
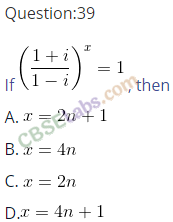

Question 40.
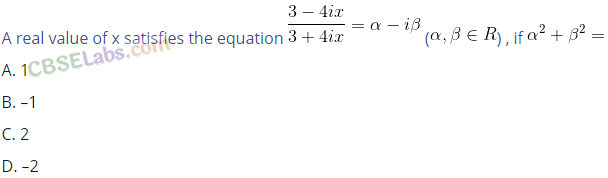
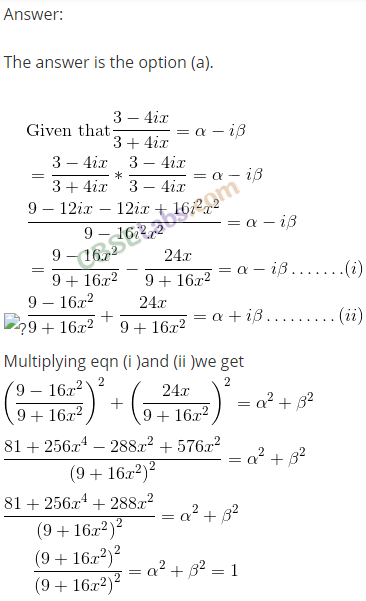
Q41. Which of the following is correct for any two complex numbers z1 and z2?
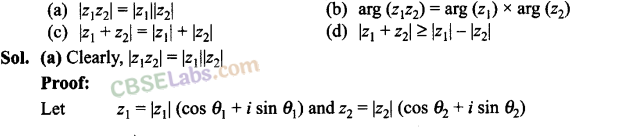
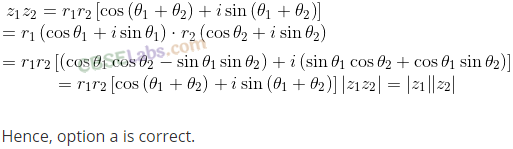
NCERT Exemplar ProblemsMathsPhysicsChemistryBiology
We hope the NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations help you. If you have any query regarding NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations, drop a comment below and we will get back to you at the earliest.
The post NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations appeared first on Learn CBSE.
NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities are part of NCERT Exemplar Class 11 Maths. Here we have given NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities.
Q1. \(\frac { 4 }{ x+1 } \le 3\le \frac { 6 }{ x+1 } \)

Q2. \(\frac { |x-2|-1 }{ |x-2|-2 } \le 0 \)
Sol: Let |x-2| = y
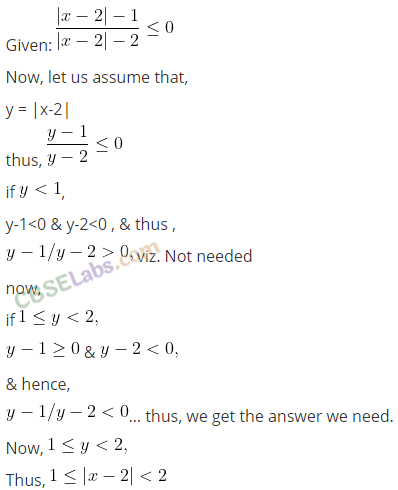

Q3. \(\frac { 1 }{ |x|-3 } \le \frac { 1 }{ 2 } \)
Sol: We have \(\frac { 1 }{ |x|-3 } \le \frac { 1 }{ 2 } \)

Q4. |x-1|≤ 5, |x| ≥ 2
Sol: |x-1|≤ 5
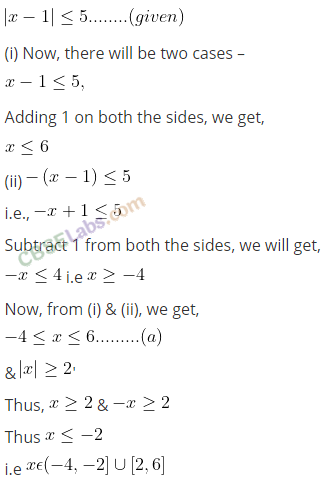
Q5. \(-5\le \frac { 2-3x }{ 4 } \le 9 \)
Sol: we have \(-5\le \frac { 2-3x }{ 4 } \le 9 \)

Q6. 4x + 3≥2x + 17, 3x – 5 < -2.
Sol: We have 4x + 3≥2x + 17

Q7. A company manufactures cassettes. Its cost and revenue functions are C(x) = 26000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week How many cassettes must be sold by the company to realise some profit?
Sol. Cost function: C(x) = 26000 + 3Ox Revenue function: R(x) = 43x For profit, R(x) > C(x)
⟹ 26000 + 30x < 43x
⟹43x – 30x > 26000
⟹ 13x> 26000
⟹ x > 2000
Hence, more than 2000 cassettes must be produced to get profit.
Q8. The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 8.2 and 8.5. If the first two pH readings are 8.48 and 8.35, find the range of pH value for the third reading that will result in the acidity level being normal.
Sol: Given, first pH value = 8.48
And second pH value = 8.35
Let third pH value be x.
Since it is given that average pH value lies between 8.2 and 8.5, we get

Q9. A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there is 460 litres of the 9% solution, how many litres of 3% solution will have to be added?
Sol: Let x Lof 3% solution be added to 460 L of 9% solution of acid.
Then, total quantity of mixture = (460 + x) L

Q10. A solution is to be kept between 40°C and 45°C. What is the range of temperature in degree Fahrenheit, if the conversion formula is F= 9/5 C + 32?
Sol. Let the required temperature be x° F

Q11. The longest side of a triangle is twice the shortest side and the third side is 2 cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm then find the minimum length of the shortest side.
Sol: Let the length of shortest side be x cm.
According to the given information,
Longest side = 2 x Shortest side = 2x cm
And third side = 2 + Shortest side = (2 + x) cm
Perimeter of triangle = x + 2x + (x + 2) = 4x + 2
But it is given that,
Perimeter > 166 cm
=> 4x + 2 > 166 => 4x> 166-2 => 4x>164
x>164/4 =41 cm
Hence, the minimum length of shortest side is 41 cm.
Q12. In drilling world’s deepest hole it was found that the temperature T in degree Celsius, jc km below the earth’s surface was given by T = 30 + 25 (x – 3), 3 ≤ x≤ At what depth will the temperature be between 155°C and 205°C?

Q13. \(\frac { 2x+1 }{ 7x-1 } >5,\frac { x+7 }{ x-8 } >2 \)


Q14. Find the linear inequalities for which the shaded region in the given figure is the solution set.
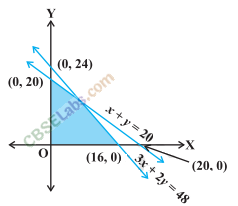
Sol: We observe that the shaded region and the origin are on the same side of the line 3x + 2y = 48.
For (0, 0), we have 3(0) + 2(0) – 48 < 0. So, the shaded region satisfies the inequality 3x + 2y≤ 48.
Also, the shaded region and the origin are on the same side of the line x+y = 20.
For (0,0), we have 0 + 0 – 20 < 0. So, the shaded region satisfies the inequality x +y ≤ 20.
Also, the shaded region lies in the first quadrant. So, x ≥0,y≥0.
Thus, the linear inequation corresponding to the given solution set are 3x + 2y ≤ 48, x + y ≤ 20 and x ≥ 0, y ≥0.
Q15Find the linear inequalities for which the shaded region in the given figure is the solution set.
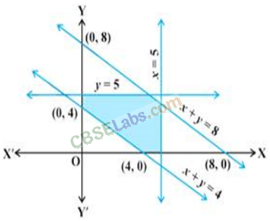
Sol: We observe that the shaded region and the origin are on the same side of the linex+y = 8.
For (0,0), we have 0 + 0 – 8 < 0. So, the shaded region satisfies the inequality x + 2≤8.
The shaded region and the origin are on the opposite side of the line x+y = 4.
For (0,0), we have 0 + 0 – 4 < 0. So, the shaded region satisfies the inequality x + 2≥4.
Further, the shaded region and the origin are on the same side of the lines x = 5 andy = 5.
So, it satisfies the inequality x ≤ 5 andy < 5.
Also, the shaded region lies in the first quadrant. So, x > 0, y > 0.
Thus, the linear inequation comprising the given solution set are: x+y≥4;x+y≤ 8;x≤ 5;y < 5;x≥ 0 andy ≥ 0.
Q16. Show that the following system of linear inequalities has no solution: x + 2y≤3, 3x + 4y> 12,x≥0,y≥ 1
Sol: We have x + 2y ≤ 3, 3x + 4y > 12, x > 0, y ≥ 1
Now let’s plot lines x + 2y = 3, 3x + 4y = 12, x = 0 and y = 1 in coordinate plane.
Line x + 2y = 3 passes through the points (0, 3/2) and (3, 0).
Line 3jc + 4y = 12 passes through points (4, 0) and (0, 3).
For (0, 0), 0 + 2(0) – 3 < 0.
Therefore, the region satisfying the inequality x + 2y ≤ 3 and (0,0) lie on the same side of the line x + 2y = 3.
For (0, 0), 3(0) + 4(0)- 12 ≤0.
Therefore, the region satisfying the inequality 3x + 4y ≥ 12 and (0, 0) lie on the opposite side of the line 3x + 4y = 12.
The region satisfying x > 0 lies to the right hand side of the y-axis.
The region satisfying y > 1 lies above the line y = 1.
These regions are plotted as shown in the following figure
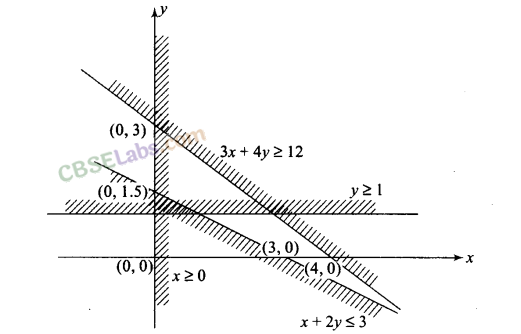
It is clear from the graph that the Shaded portions do not have common region. So, solution set is null set.
Q17. Solve the following system of linear inequalities:
3x+2y≥24,3x+y≤ 15,x≥4
Sol: We have, 3x + 2y ≥24,
3x +y ≤ 15, x ≥ 4
Now let’s plot lines 3x + 2y = 24, 3x + y = 15 and x = 4 on the coordinate plane.
Line 3x + 2y = 24 passes through the points (0, 12) and (8, 0).
Line 3x+y = 15 passes through points (5,0) and (0, 15).
Also line x = 4 is passing through the point (4, 0) and vertical.
For (0, 0), 3(0) + 2(0) – 24 < 0.
Therefore, the region satisfying the inequality 3x + 2y≥ 24 and (0, 0) lie on the opposite of the line 3x + 2y = 24.
For (0), 3(0) + (0) – 15 ≤ 0.
Therefore, the region satisfying the inequality 3x +y ≤ 15 and (0,0) lie on the same side of the line 3x +y = 15.
The region satisfying x ≥ 4 lies to the right hand side of the line x = 4.
These regions are plotted as shown in the following figure
It is clear from the graph that there is no common region corresponding to these inequalities.

Hence, the gi ven system of inequalities has no solution.
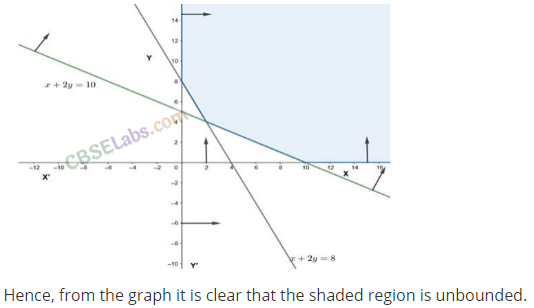
Q18. Show that the solution set of the following system of linear inequalities is an unbounded region:
2x +y ≥ 8, x + 2y > 10, x ≥ 0, y ≥ 0
Sol: We have 2x+y≥8,x + 2y> 10, x ≥ 0, y ≥ 0
Line 2x + y = 8 passes through the points (0, 8) and (4, 0).
Line x + 2y = 10 passes through points (10, 0) and (0, 5).\
For (0, 0), 2(0) + (0) – 8 < 0.
Therefore, the region satisfying the inequality 2x+y ≥ 8 and (0, 0) lie on the opposite side of the line 2x +y = 8.
For (0,0), (0) + 2(0)- 10 <0.
Therefore, the region satisfying the inequality x + 2y≥ 10 and (0,0) lie on the opposite side of the line x + 2y = 10.
Also, for x ≥ 0, y ≥0, region lies in the first quadrant.
The common region is plotted as shown in the following figure.
NCERT Exemplar ProblemsMathsPhysicsChemistryBiology</
We hope the NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities help you. If you have any query regarding NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities, drop a comment below and we will get back to you at the earliest.
The post NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities appeared first on Learn CBSE.