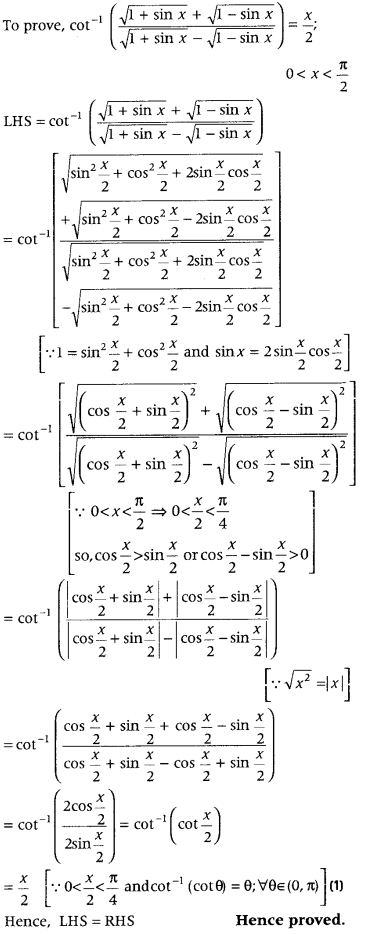
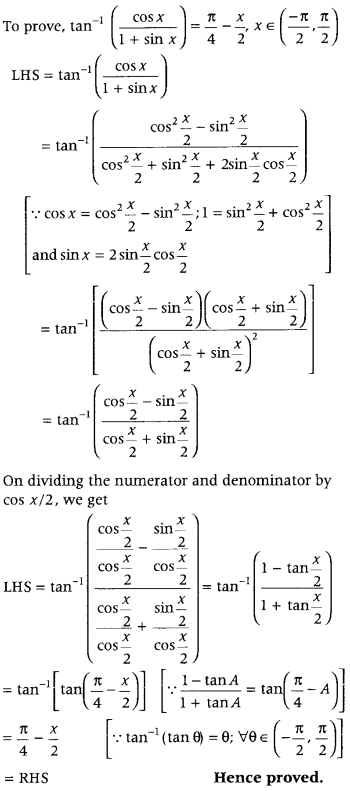
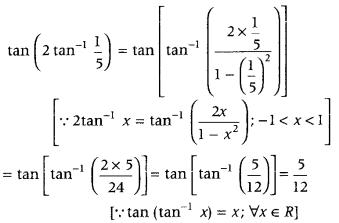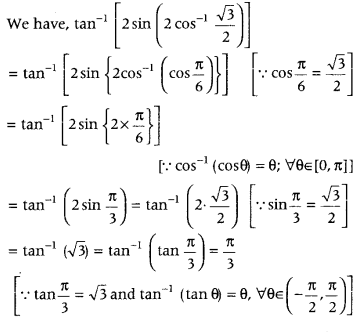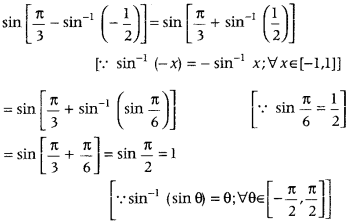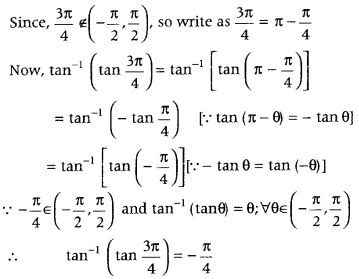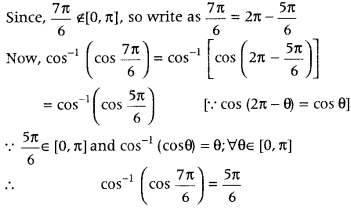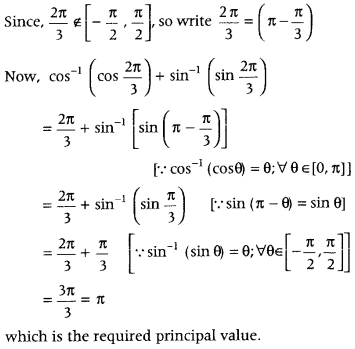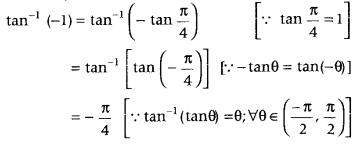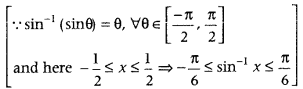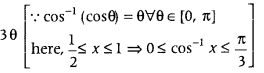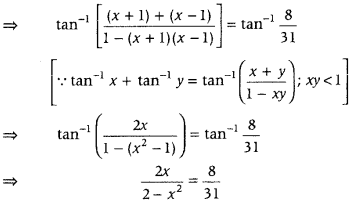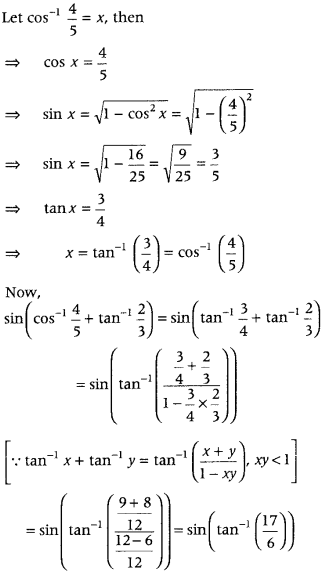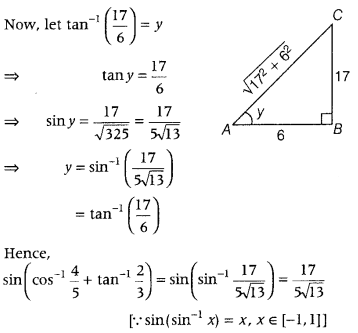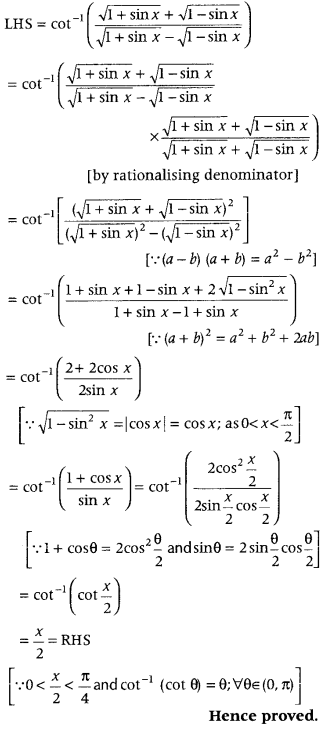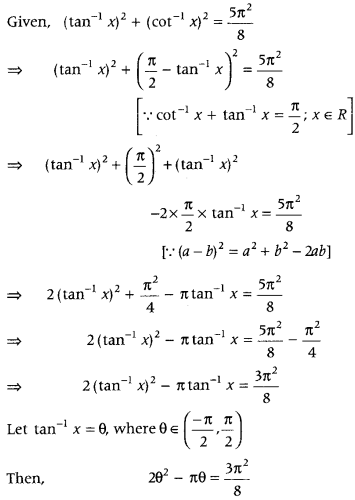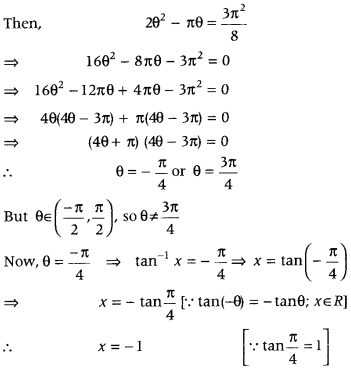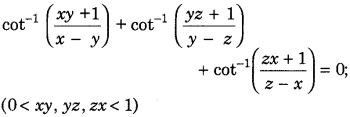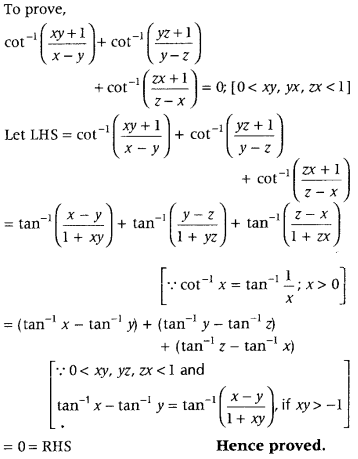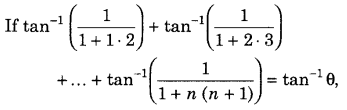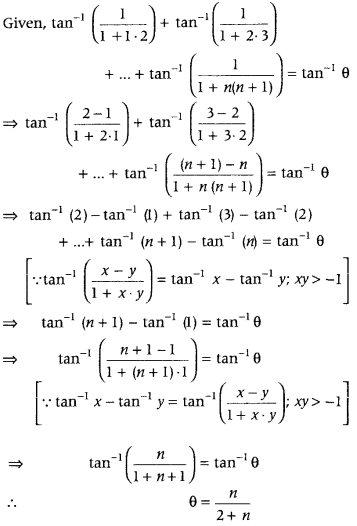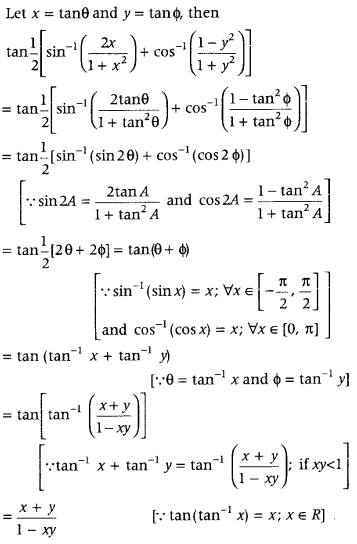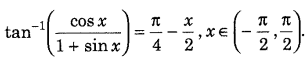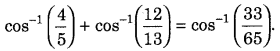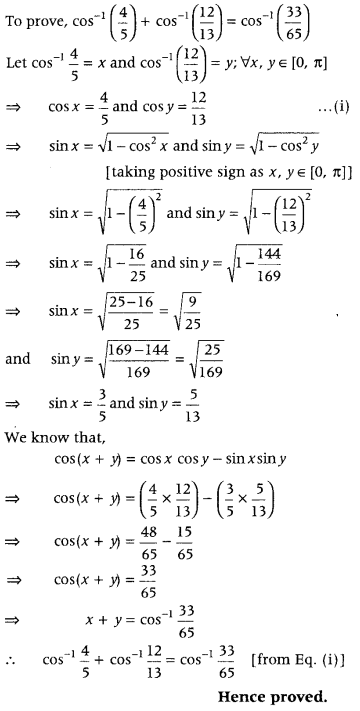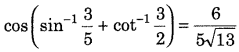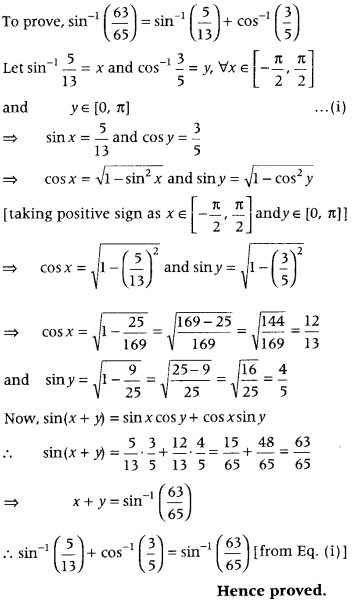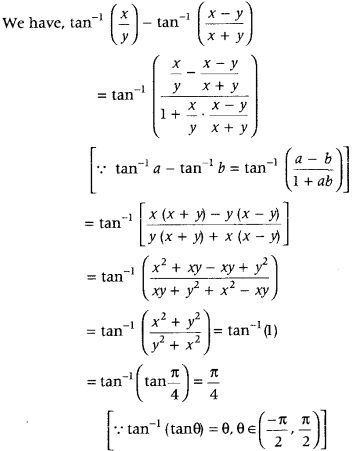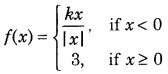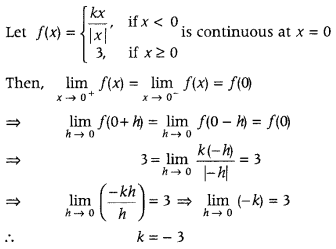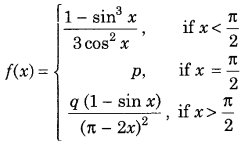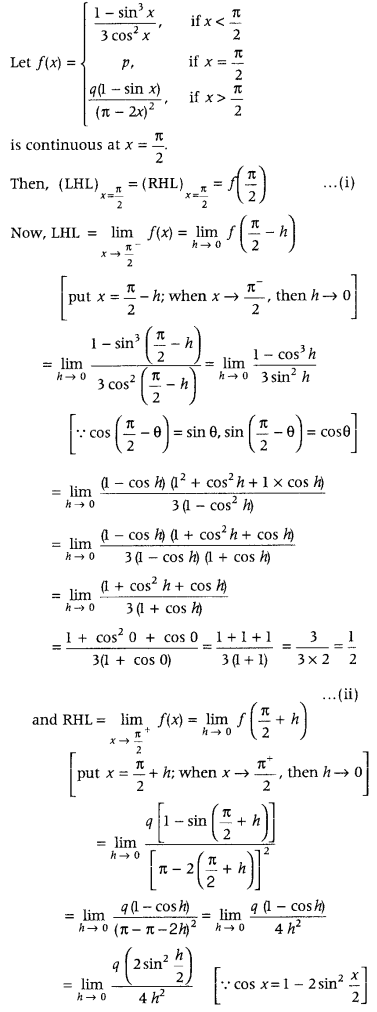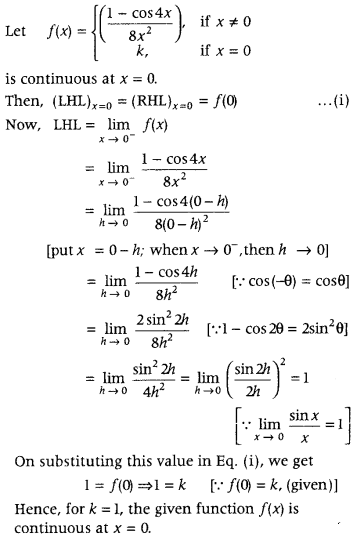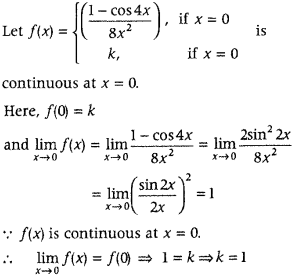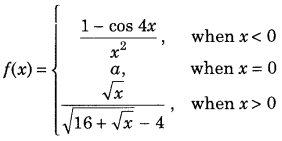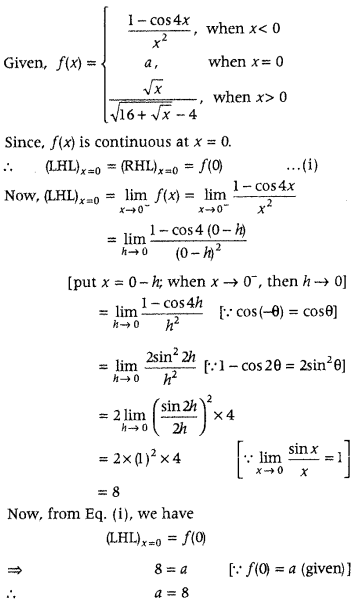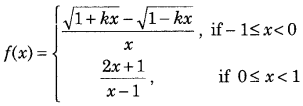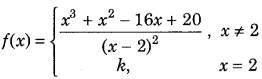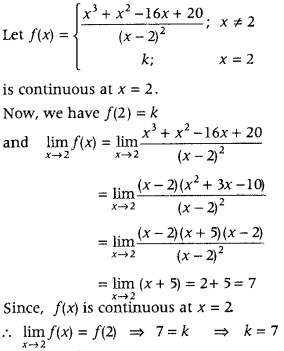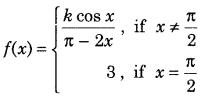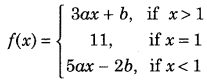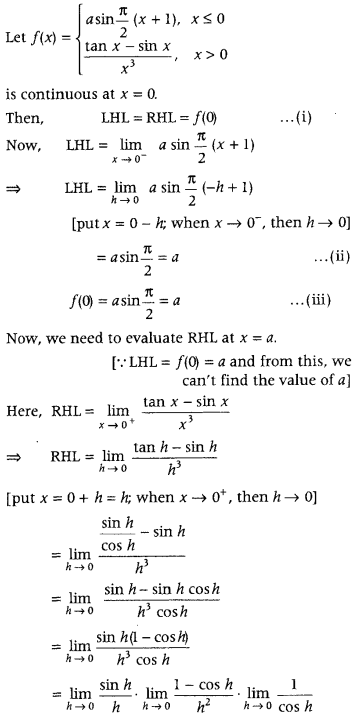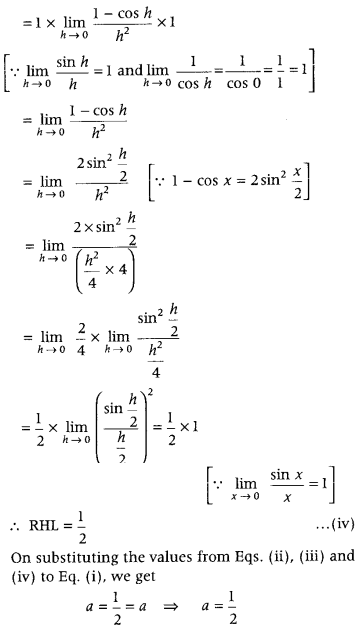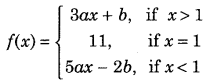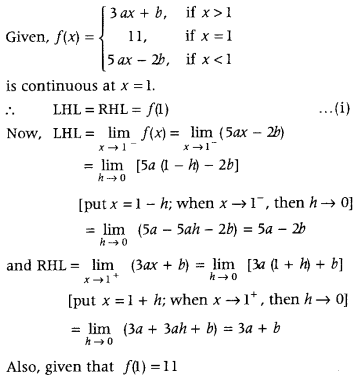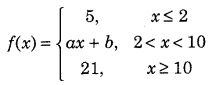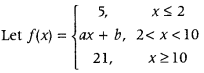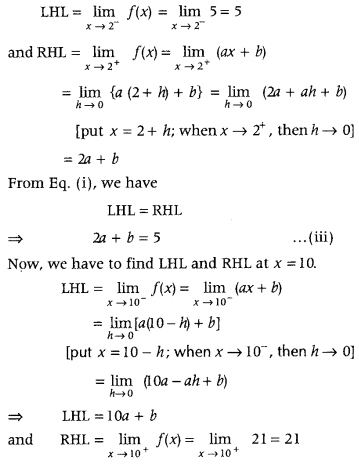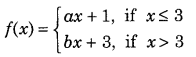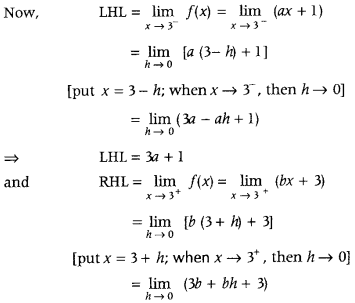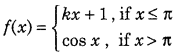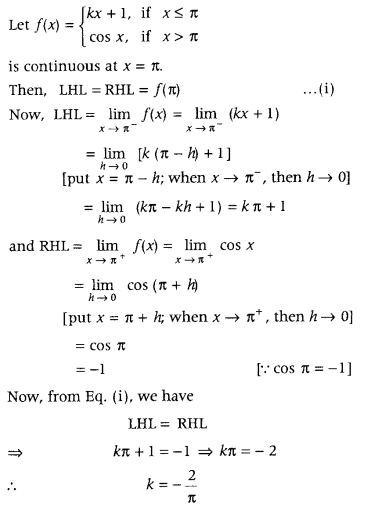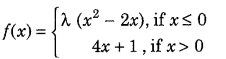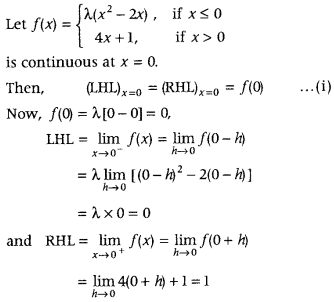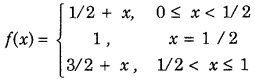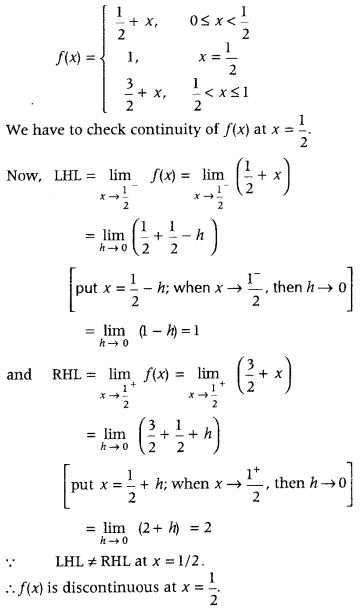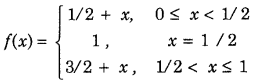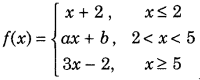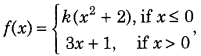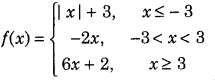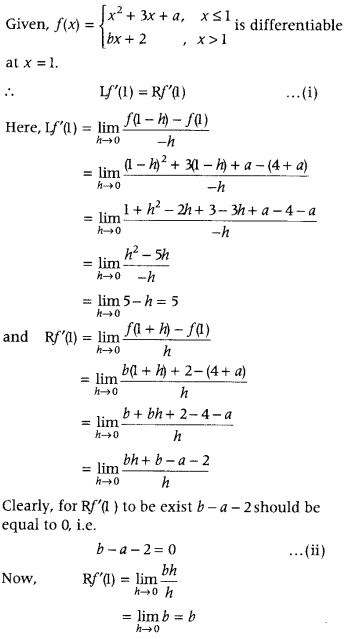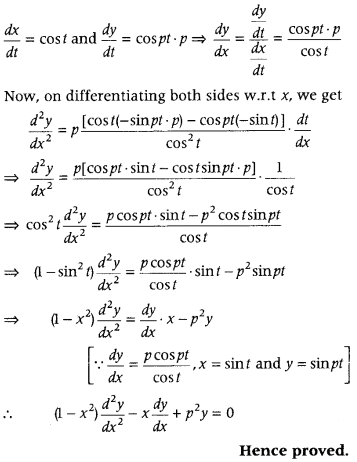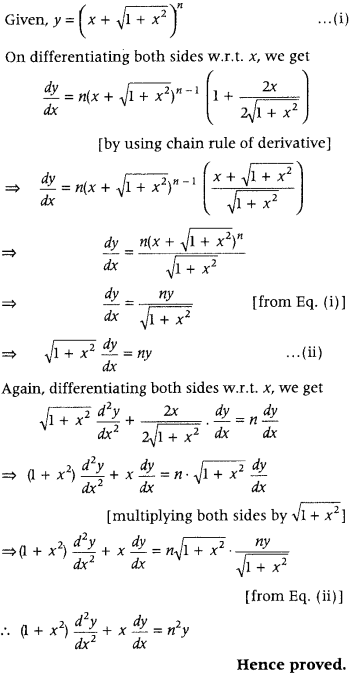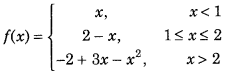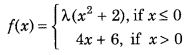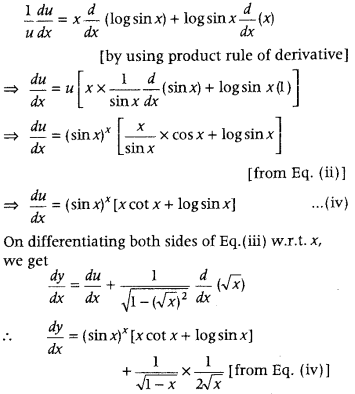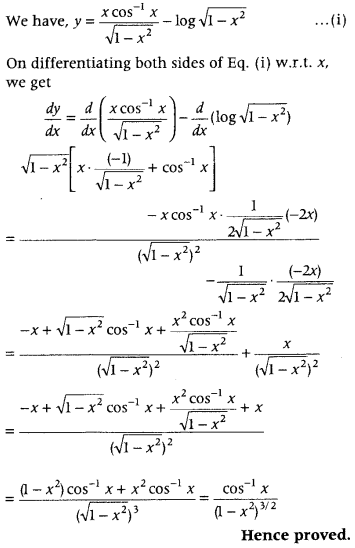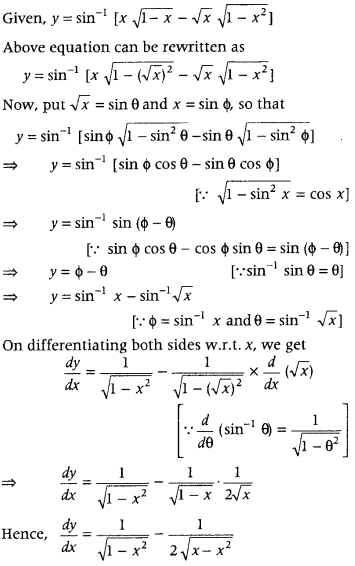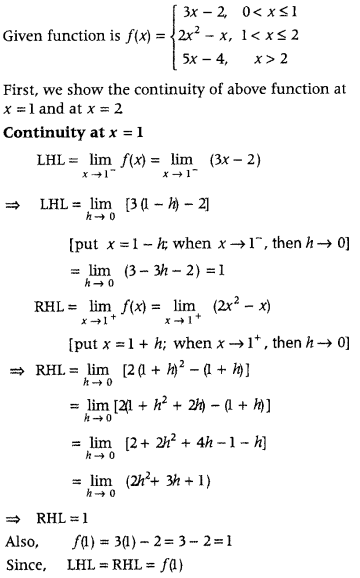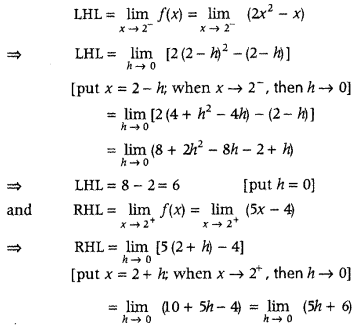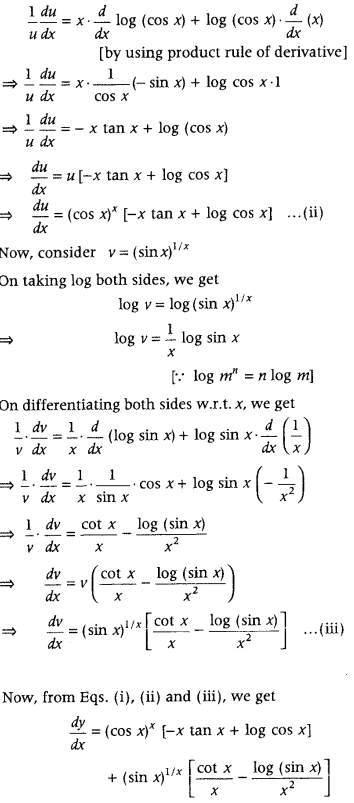Get access to Class 12 Maths Important Questions Chapter 1 Relations and Functions, Relations and Functions Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.
Relations and Functions Class 12 Important Questions with Solutions Previous Year Questions
Question 1.
If R = {(a, a3): a is a prime number less than 5} be a relation. Find the range of R . (Foreign 2014)
Answer:
Given, R = {{a, cd): a is a prime number less than 5}
We know that, 2 and 3 are the prime numbers less than 5.
So, a can take values 2 and 3.
Thus, R = {(2, 23), (3, 33)} = {(2, 8), (3, 27)}
Hence, the range of R is (8, 27}.
Question 2.
If f: {1,3, 4} → {1, 2, 5} and g: {1,2, 5} → {1, 3} given by f = {(1,2), (3, 5), (4,1)} and g = {(1,3), (2, 3), (5,1)}. Write down gof. (All India 2014C)
Answer:
Given, functions f:{1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3} are defined as f = {(1, 2),(3, 5),(4, 1)} and g = {(1, 3),(2, 3),(5, 1)}
Therefore, f(1) = 2, f(3) = 5, f(4) = 1
and g(1) = 3, g (2) = 3, g(5) = 1
Now, gof: {1,3,4} → {1,3} and it is defined as
gof (1) = g[(f(1)] = g(2) = 3
gof(3) = g[f(3)] = g(5) = 1
gof (4) = g[f(4)] = g(1) = 3
∴ gof = {(1, 3), (3, 1), (4, 3)}
Question 3.
Let R is the equivalence relation in the set A = {0,1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a – b)}. Write the equivalence class [0]. (Delhi 2014C)
Answer:
Given, R = {(a, b):2 divides(a – b)}
and A = { 0,1, 2, 3, 4, 5}
Clearly, [0] = {b ∈ A : (0, b) ∈ R}
= {b ∈ A: 2 divides (0 – b)}
= {b ∈ A : 2divides (-b)} = {0, 2, 4}
Hence, equivalence class of [0] = {0,2,4}.
Question 4.
If R = {(x, y): x + 2y = 8} is a relation on N, then write the range of R. (All India 2014)
Answer:
Given, the relation R is defined on the set of natural numbers, i.e. N as
R= {(x, y) : x + 2y = 8}
To find the range of R, x + 2y = 8 can be rewritten as y = \(\frac{8-x}{2}\)
On putting x = 2, we get y = \(\frac{8-2}{2}\) = 3
On puttmg x = 4, we get y = \(\frac{8-4}{2}\) = 2
On putting x = 6, we get y = \(\frac{8-6}{2}\) = 1
As, x, y ∈ N, therefore R = {(2, 3), (4, 2), (6, 1)}. Hence, the range of relation R is {3,2,1}.
Note: For x = 1, 3, 5, 7, 9, ……… we do not get y as natural number.
Question 5.
If A = {1, 2, 3}, S = {4, 5,6, 7} and f = {(1, 4), (2, 5), (3, 6)} is a function from A to B. State whether f is one-one or not. (All India 2011)
Answer:
5. Given, A = {1, 2, 3} , B = {4, 5, 6, 7}
and f:A → Bis defined as f = {(1, 4), (2, 5), (3, 6)}
i.e. f(1) = 4, f(2) = 5and f(3) = 6.
It can be seen that the images of distinct elements of A under f are distinct. So, f is one-one.
Question 6.
If f : R → R is defined by f{x) = 3x + 2, then define f[f(x)]. (Foreign 2011; Delhi 2010)
Answer:
Given, f(x) = 3x + 2
f[f(x)] – f(3x + 2) = 3 (3x + 2) + 2
= 9x + 6+ 2= 9x + 8
Question 7.
Write fog, if f: R → R and g:R → R are given by f(x) = |x| and g(x) = |5x – 2|. (Foreign 2011)
Answer:
Given, f(x) = |x|, g(x) = |5x – 2|
∴ fog (x) = f[g(x)] = f{15x – 2|}
= ||5x – 2||= |5x – 2| [∵ ||x|| = |x|]
Question 8.
Write fog, if f: R → R and g:R → R are given by f(x) = 8x3 and g(x) = xy3. (Foreign 2011)
Answer:
Given, f(x) = 8x3 and g(x) = x1/3
∴ fog ( x) = f[g(x)] = f(x1/3) = 8(x1/3)3 = 8x
Question 9.
State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2,1)} not to be transitive. (Delhi 2011)
Answer:
We know that for a relation to be transitive,
(x, y) ∈ R and (y, z) ∈ R ⇒ (x, z) ∈ R.
Here, (1, 2) ∈ R and (2,1) ∈ R but (1,1) ∉ R.
R is not transitive.
Question 10.
What is the range of the function.
f(x) = \(\frac{|x-1|}{x-1}\), x ≠ 1? (Delhi 2010)
Answer:
Firstly, redefine the function by using the definition of modulus function, i.e by using
![Relations and Functions Class 12 Maths Important Questions Chapter 1 1]()
Further, simplify it to get the range
Given, function is f(x) = \(\frac{|x-1|}{x-1}\), x ≠ 1
The above function can be written as
![Relations and Functions Class 12 Maths Important Questions Chapter 1 2]()
Question 11.
If f: R → R is defined by f(x) = (3 – x3)1/3, then find fof(x). (All India 2010)
Answer:
Given function is f: R → R such that f(x) = (3 – x3)1/3.
Now, fof(x) = f[f(x)] = f[(3 – x3))1/3]
= [3 – {(3 – x3)1/3}3]1/3
= [3 – (3 – x3)]1/3 = (x3)1/3 = x
Question 12.
If f is an invertible function, defined as f(x) = \(\frac{3 x-4}{5}\), then write f-1(x). (Foreign 2010)
Answer:
Given, f(x) = \(\frac{3 x-4}{5}\) is an invertible function.
![Relations and Functions Class 12 Maths Important Questions Chapter 1 3]()
Question 13.
If f : R → R and g:R → R are given by f(x) = sin x and g(x) = 5x2, then find gof(x). (Foreign 2010)
Answer:
Given, f(x) = sin x and g(x) = 5x2.
30f{x) = g[f(x)] = g(sin x)
= 5(sin x)2 = 5sin2x
Question 14.
If f(x) = 27x3 and g(x) = xy3, then find gof(x). (Foreign 2010)
Answer:
Given, f(x) = 27x3 and g(x) = xy3
Now, gof(x) = g[f(x)] = g(27x3)
= (27x3)1/3 = (27)1/3.(x3)1/3
= (33)1/3 (x3)1/3 = 3x
∴ gof(x) = 3x
Question 15.
If the function f:R → R defined by f(x) = 3x – 4 is invertible, then find f-1. (All India 2010C)
Answer:
f-1 = \(\frac{x+4}{3}\)
Question 16.
Check whether the relation R defined on the set A = {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive. (All India 2019)
Answer:
The relation R on set A = {I, 2, 3, 4, 5, 6} is defined as (a, b) ∈ R iff b = a + 1.
Therefore, R = {(1, 2),(2, 3), (3, 4), (4,5), (5, 6)}
Clearly, (a, a) ∉ R for any as a ∈ A. So, R is not reflexive on A.
We observe that (1, 2) ∈ R but (2,1) ∉ R.
So, R is not symmetric.
We also observe that (1, 2) ∈ R and (2, 3) ∈ R but (1, 3) ∉ R. So, R is not transitive.
Question 17.
Let f : N → Y be a function defined as f(x) = 4x + 3, where, Y = {y ∈ N : y = 4x + 3, for some x ∈ N}. Show that f is invertible. Find its inverse. (All India 2019)
Answer:
Given, f: N → Y defined as f(x) = 4x + 3, where
Y = {y ∈ N : y = 4x + 3, x ∈ N}. Consider an arbitrary element y ∈ Y. Then, y = 4x + 3, for some x ∈ N
⇒ y – 3 = 4x ⇒ x = \(\frac{y-3}{4}\)
Suppose, a function g:Y → N, given by
![Relations and Functions Class 12 Maths Important Questions Chapter 1 4]()
Here, gof (x) = x, ∀ x ∈ N; therefore gof = IN
and fog(y) = y, ∀ y ∈ F; therefore fog = IY
So, f is invertible and f-1 = g,
i.e f-1(y) = \(\frac{y-3}{4}\)
or f-1(x) = \(\frac{x-3}{4}\)
Question 18.
Show that the relation R on IR defined as R = {(a, b) : (a ≤ b)}, is reflexive and transitive but not symmetric. (Delhi 2019)
Answer:
Given a relation R = {{a, b): a ≤ b} on IR (the set of real numbers).
Reflexivity:
Since, a ≤ a is true for all value of a ∈ IR.
(a,a) ∈ R ∀ a ∈ IR
Hence, the given relation is reflexive.
Transitivity
Let (a, b) ∈ R and (b, c) ∈ R be any arbitrary elements.
Then, we have a ≤ b and b ≤ c
⇒ a ≤ b ≤ c
⇒ a ≤ c
⇒ (a,c) ∈ R
Hence, the given relation is transitive.
Symmetricity:
Note that (2,3) ∈ R as 2 < 3
but (3, 2) ∉ R as 3 ≮ 2
Hence, the given relation is not symmetric.
Hence proved.
Question 19.
Prove that the function, f : N → N is defined by f(x) = x2 + x + 1 is one-one but not onto. Find inverse of f : N → S, where S is range of f. (Delhi 2019)
Answer:
Let x, y ∈ N such that
f(x) = f(y)
⇒ x2 + x + 1 = y2 + y + 1
⇒ (x – y)(x + y + 1) = 0 [∵ x + y + 1 ≠ 0]
⇒ x = y
f: N → N is one-one (1)
f is not onto because x2 + x +1 > 3, ∀ x ∈ N and so, 1,2 does not have their pre images.
Now, if S is the range of f, then f:N → S is one-one, onto and hence invertible.
⇒ fof-1 (x) = x, ∀ x ∈ S
⇒ f(f-1(x)) = x, ∀ x ∈ S
⇒ (f-1(x))2 + (f-1(x)) + 1 = x, ∀ x ∈ S
⇒ (f-1(x))2 + f-1(x) + 1 – x = 0
which is quadratic in f-1(x)
![Relations and Functions Class 12 Maths Important Questions Chapter 1 5]()
Question 20.
If f: W → W is defined as f(x) = x – 1, if x is odd and f(x) = x + 1, if x is even. Show that f is invertible. Find the inverse of f, where W is the set of all whole numbers. (Foreign 2014; All India 2011C)
Answer:
Given, f: W →W is defined as
![Relations and Functions Class 12 Maths Important Questions Chapter 1 6]()
One-one function Let x1, x2 ∈ W be any two numbers such that f(x1) = f(x2)
Case I:
When x1, and x2 are odd.
Then, f(x1) = f(x2) ⇒ x1 – I = x2 – I
⇒ x1 = x2
Case II:
When x1, and x2 are even.
Then, f(x1) = f(x2)
⇒ x1 + I = x2 + I
⇒ x1 = x2
Thus, in both cases,
f(x1) = f(x2) ⇒ x1 = x2
Case III:
When x1, is odd and x2 is even.
Then, x1 ≠ x2
Also, f(x1) is even and f(x2) is odd.
So, f(x1) ≠ f(x2)
Thus, x1 ≠ x2 ⇒ f(x1) ≠ f(x2)
Case IV:
When x1 is even and x2 is odd.
Then, x1 ≠ x2
Also, f(x1) is odd and f(x2) is even.
So, f(x1) ≠ f(x2)
Thus, x1 ≠ x2 ⇒ f(x1) ≠ f(x2)
Hence, from cases I, II, III and IV we can observe that, f(x) is a one-one function.
Onto function:
Clearly, any odd number 2y + 1 in the codomain W, is the image of 2y in the domain W.
Also, any even number 2y in the codomain W, is the image of 2y + 1 in the domain W.
Thus, every element in W (codomain) has a pre-image in W (domain).
So, f is onto.
Therefore, f is bijective and so it is invertible.
Let f(x) = y
⇒ x – 1 = y, if x is odd
and x + 1 = y, if x is even
![Relations and Functions Class 12 Maths Important Questions Chapter 1 7]()
Question 21.
If f,g :R → R are two functions defined as f(x) = |x| + x and g(x) = |x| – x, ∀ x ∈ R. Then, find fog and gof. (All India 2014C)
Answer:
Given, f(x) = |x| + x and g(x) = |x| – x, ∀ x ∈ R.
![Relations and Functions Class 12 Maths Important Questions Chapter 1 8]()
Thus, for x ≥ 0,gof (x) = g(f(x)) = g(2x) = 0
and for x < 0, gof(x) = g(f(x)) = g(0) = 0 ⇒ gof(x) = 0, ∀ x ∈ R Similarly, for x > 0, fog (x) = f(g(x)) = f(0) = 0
and for x < 0, fog (x) = f(g(x)) = f(-2x)
= 2(-2x) = -4x
![Relations and Functions Class 12 Maths Important Questions Chapter 1 9]()
Question 22.
If R is a relation defined on the set of natural numbers N as follows:
R = {(x, y) : x ∈ N, y ∈ N and 2x + y = 24}, then find the domain and range of the relation R . Also, find whether R is an equivalence relation or not. (Delhi 2014C)
Answer:
Given, R = {(x, y) : x ∈ N, y ∈ N and 2x + y = 24}
∴ y = 24 – 2x
Now, x = 1 ⇒ y = 22;
x = 2 ⇒ y = 20;
x = 3 ⇒ y = 18;
x = 4 ⇒ y = 16;
x = 5 ⇒ y = 14;
x = 6 ⇒ y = 12;
x = 7 ⇒ y = 10;
x = 8 ⇒ y = 8
x = 9 ⇒ y = 6;
x = 10 ⇒ y = 4
and x = 11 ⇒ y = 2
So, domain of R= {1, 2, 3, …, 11} and range of R = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22} and R = {(1, 22), (2, 20), (3, 18), (4, 16), (5, 14), (6, 12), (7, 10), (8, 8), (9, 6), (10, 4), (11, 2)}
Reflexive:
Since, for 1 ∈ domain of R,(1, 1) ∉ R.
So, R is not reflexive.
Symmetric:
We observe that (1, 22) ∉ R but (22, 1) ∈ R. So, R is not symmetric.
Transitive:
We observe that (7, 10) ∈ Rand (10, 4) ∈ R hut (7, 4) ∉ R. So, R is not transitive. Thus, R is neither reflexive nor symmetric nor transitive.
So, R is not an equivalence relation.
Question 23.
If A = R – {3} and B = R – {1}. Consider the function f :A → B defined by f(x) = \(\frac{x-2}{x-3}\) for all x ∈ A. Then, show that f is bijective. Find f-1(x). (Delhi 2014C; Delhi 2012)
Answer:
Given, a function f: A → B, where A = R – {3}
and B = R – {1}, defined by f(x) = \(\frac{x-2}{x-3}\).
One-one function:
Let x1, x2 ∈ A such that f(x1) = f(x2)
Then \(\frac{x_{1}-2}{x_{1}-3}=\frac{x_{2}-2}{x_{2}-3}\)
⇒ (x1 – 2)(x1 – 3) = (x2 – 2)(x1 – 3)
⇒ x1x2 – 3x1 – 2x2 + 6 = x1x2 – 3x2 – 21 + 6
⇒ – 3x1 – 2x2 = – 3x2 – 2x1
⇒ – 3 (x1 – x2) + 2 (x1 – x2) = 0
⇒ -(x1 – x2) = 0
Thus, f(x1) = f(x2)
⇒ x1 = x2, ∀ x1, x2 ∈ A
So, f(x) is a one-one function.
Onto function:
Let y ∈ B = R – {1} be any arbitrary element.
Then, f(x) = y
⇒ \(\frac{x-2}{x-3}\) = y ⇒ x – 2 = xy – 3y
⇒ x – xy = 2 – 3y
⇒ x(1 – y) = 2 – 3y
⇒ x = \(\frac{2-3 y}{1-y}\) or x = \(\frac{3 y-2}{y-1}\) ………(i)
Clearly, x = \(\frac{3 y-2}{y-1}\) is a real number for all y ≠ 1.
![Relations and Functions Class 12 Maths Important Questions Chapter 1 10]()
Hence, f(x) is an onto function.
Therefore, f(x) is a bijective function.
From Eq. (i), we get
f-1(y) = \(\frac{3 y-2}{y-1}\) or f-1(x) = \(\frac{3 x-2}{x-1}\)
which is the inverse function of f(x).
Question 24.
If A = {1, 2, 3, .. ,9} and R is the relation in A × A defined by (a , b) R(c, d), if a + d = b + c for (a,b), (c, d) in A × A. Prove that R is an equivalence relation. Also, obtain the equivalence class [(2, 5)]. (Delhi 2014)
Answer:
Given a relation R in A × A, where A = {1, 2, 3,…, 9}, defined as (a, b) R (c, d), if a + d = b + c.
Reflexive:
Let (a, b) be any arbitrary element of A × A. i.e. (a, b) ∈ A × A, where a,b ∈ A.
Now, as a + b = b + a [∵ addition is commutative]
∴ (a, b) R{a, b)
So, R is reflexive.
Symmetric:
Let (a, b), (c,d)e Ax A, such that (a, b)R(c, d). Then, a + d = b + c
⇒ b + c = a + d ⇒ c + b = d + a [∵ addition is commutative]
⇒ (c, d) R(a, b)
So, R is symmetric.
Transitive:
Let (a, b), (c, d), (e, f) ∈ A × A such that (a, b) R(c, d) and (c, d) R(e, f).
Then, a + d = b + c and c + f = d + e
On adding the above equations,
we get a + d + c + f = b + c + d + e
⇒ a + f = b + e ⇒ (a, b) R(e, f)
So, R is transitive.
Thus, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.
Now, for [(2, 5)], we will find (c, d) ∈ A × A such that 2 + d = 5+ c or d-c = 3 (1/2)
Clearly, (2, 5) R(1, 4) as 4 – 1 = 3
(2, 5) R(2, 5) as 5 – 2 = 3
(2, 5) R(3, 6) as 6 – 3 = 3
(2, 5) R(4, 7) as 7 – 4 = 3
(2, 5) R(5, 8) as 8 – 5 = 3
and (2, 5) R(6, 9) as 9 – 6 = 3
Hence, equivalence class [(2, 5)]
= {(1, 4), (2, 5),(3, 6),(4, 7),(5, 8),(6, 9)}.
Question 25.
If the function R → R is given by f(x) = x2 + 2 and g:R → R is given by g(x) = \(\frac{x}{x-1}\), then find fog and gof, and hence find fog (2) and gof (- 3). (All India 2014)
Answer:
Given, f : R → R and g : R → R defined as
f(x) = x2 + 2 and g(x) = \(\frac{x}{x-1}\); x ≠ 1
Since, range f ⊆ domain g and range g ⊆ domain f
∴ fog and gof exist.
For any x ∈ R- {1}, we have (fog)(x) = f[g(x)]
![Relations and Functions Class 12 Maths Important Questions Chapter 1 11]()
Question 26.
If A = R-{2}, B = R-{1} and f: A → B is a function defined by f(x) = \(\frac{x-1}{x-2}\) , then show that f is one-one and onto. Hence, find f-1. (Delhi 2013C)
Answer:
f-1 = \(\frac{2 x-1}{x-1}\)
Question 27.
Show that the function f in A = R – \(\left\{\frac{2}{3}\right\}\) defined as f(x) = \(\frac{4 x+3}{6 x-4}\) is one-one and onto. Hence, find f-1. (Delhi 2013)
Answer:
Given f(x) = \(\frac{4 x+3}{6 x-4}\)
where, x ∈ A = R – \(\left\{\frac{2}{3}\right\}\)
One-one function:
Let x1, x2 ∈ A = R – \(\left\{\frac{2}{3}\right\}\) such that f(x1) = f(x2).
Then, \(\frac{4 x_{1}+3}{6 x_{1}-4}=\frac{4 x_{2}+3}{6 x_{2}-4}\)
⇒ (4x1 + 3) (6x2 – 4) = (4x2 + 3) (6x2 – 4)
⇒ 24x1x2 – 16x1 + 18x2 – 12 = 24x1x2 – 16x2 + 18x1 – 12
⇒ – 34x1 = – 34x2
⇒ x1 = x2
So, f is one-one function.
Onto function:
Let y be an arbitrary element of A (codomain).
Then, f(x) = y
⇒ \(\frac{4 x+3}{6 x-4}\) = y
⇒ 4x + 3 = 6xy – 4y
⇒ 4x – 6xy = -4y – 3
⇒ x(4 – 6 y) = -(4y + 3)
⇒ x = \(\frac{-(4 y+3)}{4-6 y}\)
⇒ x = \(\frac{4 y+3)}{6 y-4}\)
Clearly, x = \(\frac{4 y+3)}{6 y-4}\) is a reaj number for all y ≠ \(\frac{4}{6}=\frac{2}{3}\)
![Relations and Functions Class 12 Maths Important Questions Chapter 1 12]()
Thus, for each y ∈ A (codomain), there exists
x = \(\frac{4 x+3}{6 x-4}\) ∈ A (domain) such that
![Relations and Functions Class 12 Maths Important Questions Chapter 1 13]()
Hence, f is onto function.
Since, f is bijective function, so its inverse exists.
![Relations and Functions Class 12 Maths Important Questions Chapter 1 14]()
Question 28.
Consider f: R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is invertible with the inverse f-1 of f given by f-1(y) = \(\sqrt{y-4}\), where R+ is the set of all non-negative real numbers. (All India 2013; Foreign 2011)
Answer:
To show f(x) is an invertible function, we will show that f is both one-one and onto function.
Here, function f: R+ → [4, ∞) given by f(x) = x2 + 4.
One-one function:
Let x, y ∈ R+, such that
f(x) = f(y)
⇒ x2 + 4 = y2 + 4 ⇒ x2 = y2 ⇒ x = y
[∵ we take only positive sign as x, y ∈ R+]
Therefore, f is a one-one function.
Onto function:
For y ∈ [4, ∞), then there exists x ∈ R+ such that f(x) = y
⇒ y = x2 + 4
⇒ x2 = y – 4 ≥ 0 [∵ y > 4]
⇒ x = \(\sqrt{y-4}\) ≥ 0
[we take only positive sign, as x ∈ R+]
Therefore, for any y ∈ R+ (codomain), there exists x = \(\sqrt{y-4}\) ∈ R+ (domain) such that f(x) = \((\sqrt{y-4})=(\sqrt{y-4})^{2}\) + 4 = y – 4 + 4 = y
Therefore, f is onto function.
Since, f is one-one and onto and therefore f-1 exists.
Alternate Method:
Let us define g: [4, ∞) → R+
by g(y) = \(\sqrt{y-4}\)
Now, gof(x) = 4 (f(x)) = g(x2 + 4)
= \(\sqrt{\left(x^{2}+4\right)-4}=\sqrt{x^{2}}\) = x
and fog(y) = f[g(y)] = f(\(\sqrt{y-4}\))
= \((\sqrt{y-4})^{2}\) + 4 = (y – 4) + 4 = y
Thus, gof = I R+ and fog = I[4, ∞)
⇒ f is invertible and its inverse function is 5.
∴ f-1(y) = g(y) = \(\sqrt{y-4}\) or f-1(x) = \(\sqrt{x-4}\)
Question 29.
Show that f: N → N, given by
![Relations and Functions Class 12 Maths Important Questions Chapter 1 15]()
is bijective (both one-one and onto). (All India 2012)
Answer:
Given function is f: N → N such that
![Relations and Functions Class 12 Maths Important Questions Chapter 1 15]()
One-one function:
Let x1, x2 ∈ W be any two numbers such that f(x1) = f(x2)
Case I:
When x1, and x2 are odd.
Then, f(x1) = f(x2) ⇒ x1 – I = x2 – I
⇒ x1 = x2
Case II:
When x1, and x2 are even.
Then, f(x1) = f(x2)
⇒ x1 + I = x2 + I
⇒ x1 = x2
Thus, in both cases,
f(x1) = f(x2) ⇒ x1 = x2
Case III:
When x1, is odd and x2 is even.
Then, x1 ≠ x2
Also, f(x1) is even and f(x2) is odd.
So, f(x1) ≠ f(x2)
Thus, x1 ≠ x2 ⇒ f(x1) ≠ f(x2)
Case IV:
When x1 is even and x2 is odd.
Then, x1 ≠ x2
Also, f(x1) is odd and f(x2) is even.
So, f(x1) ≠ f(x2)
Thus, x1 ≠ x2 ⇒ f(x1) ≠ f(x2)
Hence, from cases I, II, III and IV we can observe that f(x) is a one-one function.
Onto function:
Let y ∈ N (codomain) be any arbitrary number.
If y is odd, then there exists an even number y + 1 ∈ N (domain) such that
f(y + 1) = (y + 1) – 1 = y
If y is even, then there exists an odd number y – 1 ∈ N (domain) such that
f(y – 1) = (y – 1) + 1 = y
Thus, every element in N (codomain) has a pre-image in N (domain).
Therefore, f(x) is an onto function.
Hence, the function f(x) is bijective.
Question 30.
If f: R → R is defined as f(x) = 10x + 7. Find the function g :R → R, such that gof = fog = IR. (All India 2011)
Answer:
Firstly, consider gof(x) = IR(x), further let f(x) is y equal to y and then transform x into y. Finally replace y by x.
Given, f(x) = 10x + 7
Also, gof = fog = IR
Now, gof = IR ⇒ gof(x) = IR(x)
⇒ g [f(x)] = x, ∀ x ∈ R [∵ IR(x) = x,Vxek]
⇒ g (10x + 7) = x, ∀ x ∈ R
Let 10x+ 7 = y => 10x = y-7
x = \(\frac{y-7}{10}\) ⇒ g(y) = \(\frac{y-7}{10}\), ∀ y ∈ k,
or g(x) = \(\frac{y-7}{10}\), ∀ x ∈ k
Question 31.
If f: R → R is the function defined by f(x) = 4x3 + 7, then show that f is a bijection. (Delhi 2011C)
Answer:
The given function is f: R → R such that f(x) = 4x3 + 7
To show f is bijective, we have to show that f is one-one and onto.
One-one function:
Let x1, x2 ∈ R such that f(x1) = f(x2)
⇒ 4x13 + 7 = 4x23 + 7
⇒ 4x13 = 4x23 13 x13 – x23 = 0
⇒ (x1 – x2) (x12 + x1x2 + x22) = 0
⇒ (x1 – x2)[(x1 + \(\frac{x_{2}}{2}\))2 + \frac{3}{4}22] = 0
⇒ Either x1 – x2 = 0 …………..(i)
0r (x1 + \(\frac{x_{2}}{2}\))2 + \frac{3}{4}22 = 0 …………(ii)
But Eq. (ii) gives complex roots as x1, x2 ∈ R.
∴ x1 – x2 = 0 ⇒ x1 = x2
Thus, f(x1) = f(x2) ⇒ x1 = x2, ∀ x1, x2 ∈ R
Therefore, f(x) is a one-one function.
Onto function:
Let ye R (codomain) be any arbitrary number.
Then, f(x) = y ⇒ 4x3 + 7 = y ⇒ 4x3 = y – 7
⇒ x3 = \(\frac{y-7}{4}\) ⇒ x = \(\left(\frac{y-7}{4}\right)^{1 / 3}\)
which is a real number. [∵ y ∈ R]
Thus, for every y ∈ R (codomain), there exists
![Relations and Functions Class 12 Maths Important Questions Chapter 1 16]()
⇒ f(x) is an onto function.
Since, f(x) is both one-one and onto, so it is a bijective.
Question 32.
If Z is the set of all integers and R is the relation on Z defined as R = {(a, b):a,b ∈ Z and a – b is divisible by 5}. Prove that R is an equivalence relation. (Delhi 2010)
Answer:
The given relation is R = {(a, b): a, b ∈ Z and a – b is divisible by 5}.
To prove R is an equivalence relation, we have to prove R is reflexive, symmetric and transitive.
Reflexive:
As for any x ∈ Z, we have x – x = 0, which is divisible by 5.
⇒ (x – x) is divisible by 5.
⇒ (x, x) ∈ R, V x ∈ Z Therefore, R is reflexive.
Symmetric:
Let (x, y) ∈ R, where x, y ∈ Z.
⇒ (x – y) is divisible by 5. [by definition of R]
⇒ x – y = 5A for some A ∈ Z.
⇒ y – x = 5(-A)
⇒ (y – x) is also divisible by 5.
⇒ (y, x) ∈ R
Therefore, R is symmetric.
Transitive:
Let (x, y) ∈ R,where x, y ∈ Z.
⇒ (x – y) is divisible by 5.
⇒ x – y = 5Afor some A ∈ Z Again, let (y, z) ∈ R, where y, z ∈ Z.
⇒ (y – 1) is divisible by 5.
⇒ y – z = 5B for some B ∈ Z.
Now, (x – y) + (y – 2) = 5A + 5B
⇒ x – z = 5(A + B)
⇒ (x – z) is divisible by 5 for some (A + B) ∈ Z
⇒ (x, z) ∈ R
Therefore, R is transitive.
Thus, R is reflexive, symmetric and transitive. Hence, it is an equivalence relation.
Note: If atleast one of the conditions, i.e. reflexive, symmetric and transitive, is not satisfied, then we say that the given relation is not an equivalence relation.
Question 33.
Show that the relation S in the set R of real numbers defined as S – {(a, b): a,b ∈ R and a ≤ b3} is neither reflexive nor symmetric nor transitive. (Delhi 2010)
Answer:
Here, the result is disproved by using some specific examples.
Given relation is
S = {(a, b) : a, b ∈ R and a ≤ b3}
Reflexive:
As \(\frac{1}{2} \leq\left(\frac{1}{2}\right)^{3}\), where \(\frac{1}{2}\) ∈ R, is not true
∴ \left(\frac{1}{2}, \frac{1}{2}\right) ∉ S
Therefore, S is not symmetric. (1)
Transitive:
As 3 ≤ \(\left(\frac{3}{2}\right)^{3}\) and \(\frac{3}{2} \leq\left(\frac{4}{3}\right)^{3}\) where 3, \(\frac{3}{2}, \frac{4}{3}\) ∈ S are true but 3 ≤ \(\left(\frac{4}{3}\right)^{3}\)
i.e (3, \(\frac{3}{2}\)) ∈ S and \(\left(\frac{3}{2}, \frac{4}{3}\right)\) ∈ S but (3, \(\frac{4}{3}\)) ∉ S
Therefore, S is not transitive.
Hence, S is neither reflexive nor symmetric nor transitive.
Question 34.
Show that the relation S in set A = {x ∈ Z: 0 ≤ x ≤ 12} given by S = {(a, b): a, b ∈ |a – b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. (All India 2010)
Answer:
Given relation is S = {(a, b): |a – b| is divisible by 4 and a, b ∈ A}
and A = {x : x ∈ Z and 0 ≤ x ≤ 12}
Now, A can be written as
A = {0,1, 2, 3, …,12}
Reflexive:
As for any x ∈ A, we get |x – x| = 0, which is divisible by 4.
⇒ (x, x) ∈ S, ∀ x ∈ A
Therefore, S is reflexive.
Symmetric:
As for any (x, y) ∈ S, we get |x – y| is divisible by 4. [by using definition of given relation]
⇒ |x – y| = 4λ, for some λ ∈ Z
⇒|y- x| = 4λ, for some λ ∈ Z
⇒ (y, x) ∈ S
Thus, (x, y) ∈ S ⇒ (y, x) ∈ S, ∀ x, y ∈ A
Therefore, S is symmetric.
Transitive:
For any (x, y) ∈ S and (y, z) ∈ S, we get |x – y| is divisible by 4 and |y – z| is divisible by 4. [by using definition of given relation]
⇒ |x – y| = 4λ and |y – z| = 4μ, for some λ, μ ∈ Z.
Now, x – z = (x – y) + (y – z)
= ± 4λ + 4μ
= ± 4 (λ, + μ)
⇒ |x – z| is divisible by 4.
⇒ (x, z) ∈ S
Thus, (x, y) ∈ S and (y, z) ∈ S
=* (x, z) ∈ S, ∀ x, y, z ∈ A
Therefore, S is transitive.
Since, S is reflexive, symmetric and transitive, so it is an equivalence relation. Now, set of all elements related to 1 is {1,5,9}.
Question 35.
Show that the relation S defined on set N × N by (a, b) S (c, d) ⇒ a + d = b + c is an equivalence relation. (All India 2010)
Answer:
Given a relation R in A × A, where A = {1, 2, 3,…, 9}, defined as (a, b) R (c, d), if a + d = b + c.
Reflexive:
Let (a, b) be any arbitrary element of A × A. i.e. (a, b) ∈ A × A, where a,b ∈ A.
Now, as a + b = b + a [∵ addition is commutative]
∴ (a, b) R{a, b)
So, R is reflexive.
Symmetric:
Let (a, b), (c,d) ∈ A × A, such that (a, b)R(c, d). Then, a + d = b + c
⇒ b + c = a + d ⇒ c + b = d + a [∵ addition is commutative]
⇒ (c, d) R(a, b)
So, R is symmetric.
Transitive:
Let (a, b), (c, d), (e, f) ∈ A × A such that (a, b) R(c, d) and (c, d) R(e, f).
Then, a + d = b + c and c + f = d + e
On adding the above equations,
we get a + d + c + f = b + c + d + e
⇒ a + f = b + e ⇒ (a, b) R(e, f)
So, R is transitive.
Thus, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.
Now, for [(2, 5)], we will find (c, d) ∈ A × A such that 2 + d = 5+ c or d-c = 3 (1/2)
Clearly, (2, 5) R(1, 4) as 4 – 1 = 3
(2, 5) R(2, 5) as 5 – 2 = 3
(2, 5) R(3, 6) as 6 – 3 = 3
(2, 5) R(4, 7) as 7 – 4 = 3
(2, 5) R(5, 8) as 8 – 5 = 3
and (2, 5) R(6, 9) as 9 – 6 = 3
Hence, equivalence class [(2, 5)]
= {(1, 4), (2, 5),(3, 6),(4, 7),(5, 8),(6, 9)}.
Question 36.
If f : X → Y is a function. Define a relation R on X given by R = {(a, b): f(a) = f(b)}. Show that R is an equivalence relation on X. (All India 2010C)
Answer:
The given function is f: X → Y and relation on X is R = {(a, b): f(a) = f(b)}
Reflexive:
Since, for every x ∈ X, we have
f(x) = f(x)
⇒ (x, x) ∈ R, ∀ x ∈ X
Therefore, R is reflexive.
Symmetric:
Let (x, y) ∈ R
Then, f(x) = f(y) ⇒ f(y) = f(x) ⇒ (x, y) ∈ R
Thus, (x, y) ∈ R ⇒ (y, x) ∈ R, ∀ x, y ∈ X
Therefore, R is symmetric.
Transitive:
Let x, y, z ∈ X such that
(x, y) ∈ S and (y, z) ∈ R
Then f(x) = f(y) ………..(i)
and f(y) = f(z) ………..(ii)
From Eqs. (i) and (ii), we get
f(x) = f(y)
⇒ (x, z) ∈ R
Thus, (x, y) ∈ R and (y, z) ∈ R
⇒ (x, z) ∈ R, ∀ x, y, z ∈ X
Therefore, R is transitive.
Since, R is reflexive, symmetric and transitive, so it is an equivalence relation.
Question 37.
Show that a function f: R → R given by f(x) = ax + b, a, b ∈ R, a ≠ 0 is a bijective. (Delhi 2010C)
Answer:
Given function f: R → R is such that f(x) = ax + b, a, b ∈ R, a ≠ 0
One-one function:
Let x1, x2 ∈ S such that
f(x1) = f(x2)
Then, ax1 + b = ax2 + b
⇒ ax1 = ax2
x1 = x2 [∵ a ≠ 0]
Thus, f(x1) = f(x2) ⇒ x1 = x2, ∀ x1, x2 ∈ R
Therefore, f(x) is a one-one function.
Onto function:
Let y ∈ R (codomain) be any arbitrary element.
Then, f(x) = y ⇒ ax + b = y
⇒ x = \(\frac{y-b}{a}\)
Clearly, x is a real number. [∵ y ∈ R]
Thus, for each y ∈ R (codomain), there exists x = \(\frac{y-b}{a}\) ∈ R (domain) such that
f(x) = f\(\left(\frac{y-b}{a}\right)\) = a\(\left(\frac{y-b}{a}\right)\) + b = y – b + b = y
Therefore, f(x) is an onto function.
As f(x) is both one-one and onto, so it is a bijective function.
Question 38.
Let A = {x ∈ Z: 0 ≤ x ≤ 12}. Show that R = {(a, b): a, b ∈ A, |a – b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also, write the equivalence class [2]. (CBSE 2018)
Answer:
The set of all elements related to [2]
= {a ∈ A : |2 – a| is divisible by 4}
= {2, 6,10}
(Given relation is S = {(a, b): |a – b| is divisible by 4 and a, b ∈ A}
and A = {x : x ∈ Z and 0 ≤ x ≤ 12}
Now, A can be written as
A = {0,1, 2, 3, …,12}
Reflexive:
As for any x ∈ A, we get |x – x| = 0, which is divisible by 4.
⇒ (x, x) ∈ S, ∀ x ∈ A
Therefore, S is reflexive.
Symmetric:
As for any (x, y) ∈ S, we get |x – y| is divisible by 4. [by using definition of given relation]
⇒ |x – y| = 4λ, for some λ ∈ Z
⇒|y- x| = 4λ, for some λ ∈ Z
⇒ (y, x) ∈ S
Thus, (x, y) ∈ S ⇒ (y, x) ∈ S, ∀ x, y ∈ A
Therefore, S is symmetric.
Transitive:
For any (x, y) ∈ S and (y, z) ∈ S, we get |x – y| is divisible by 4 and |y – z| is divisible by 4. [by using definition of given relation]
⇒ |x – y| = 4λ and |y – z| = 4μ, for some λ, μ ∈ Z.
Now, x – z = (x – y) + (y – z)
= ± 4λ + 4μ
= ± 4 (λ, + μ)
⇒ |x – z| is divisible by 4.
⇒ (x, z) ∈ S
Thus, (x, y) ∈ S and (y, z) ∈ S
=* (x, z) ∈ S, ∀ x, y, z ∈ A
Therefore, S is transitive.
Since, S is reflexive, symmetric and transitive, so it is an equivalence relation. Now, set of all elements related to 1 is {1,5,9}.)
Question 39.
Show that the function f: R → R defined by f(x) = \(\frac{x}{x^{2}+1}\), ∀ x ∈ R is neither one-one nor onto. Also, if g: R → R is defined as g(x) = 2x – 1, find fog (x). (CBSE 2018)
Answer:
We have, a function f: R → R defined by
f(x) = \(\frac{x}{x^{2}+1}\), ∀ x ∈ R
To show f is neither one-one nor onto.
(i) One-one:
Let x1, x2 ∈ R such that
f(x1) = f(x2)
⇒ \(\frac{x_{1}}{x_{1}^{2}+1}=\frac{x_{2}}{x_{2}^{2}+1}\)
⇒ x1 (x22 + 1) = x2(x12 + 1)
⇒ x1x22 + x1 = x2x12 + x2
⇒ x1x2(x2 – x1) = (x2 – x1)
⇒ (x2 – x1)(x1x2 – 1) = 0
⇒ x2 = x1 or x1x2 = 1
⇒ x1 = x2 or x1 = \(\frac{1}{x_{2}}\)
Here, f is not one-one as if we take.
In particular, x1 = 2 and x2 = \(\frac{1}{2}\), we get
![Relations and Functions Class 12 Maths Important Questions Chapter 1 17]()
∴ f is not one-one.
(ii) Onto:
Let y ∈ R (codomain) be any arbitrary element.
Consider, y = f(x)
∴ y = \(\frac{x}{x^{2}+1}\) ⇒ x2y + y = x
⇒ x2y – x + y = 0
⇒ x = \(\frac{1 \pm \sqrt{I-4 y^{2}}}{2 y}\), which does not exist for
1 – 4y2 < 0, i.e for y > \(\frac{1}{2}\) and y < \(\frac{-1}{2}\)
In particular for y = 1 ∈ R (codomain), there does not exist any x ∈ R (domain) such that f(x) = y. f is not onto. Hence, f is neither one-one nor onto. Now, it is given that g :R → R defined as g(x) = 2x – 1 g(x) = 2x – 1
![Relations and Functions Class 12 Maths Important Questions Chapter 1 18]()
Question 40.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ R ⇔ (x – y) is divisible by 3 is an equivalence relation. (CBSE 2018C)
Answer:
The given relation is R = {(a, b): a, b ∈ Z and a – b is divisible by 5}.
To prove R is an equivalence relation, we have to prove R is reflexive, symmetric and transitive.
Reflexive:
As for any x ∈ Z, we have x – x = 0, which is divisible by 5. ⇒ (x – x) is divisible by 5.
⇒ (x, x) ∈ R, V x ∈ Z Therefore, R is reflexive.
Symmetric:
Let (x, y) ∈ R, where x, y ∈ Z. ⇒ (x -y) is divisible by 5. [by definition of R]
⇒ x – y = 5A for some A Z. ⇒ y-x = 5(-A) ⇒ (y- x) is also divisible by 5.
⇒ (y, x) ∈ R
Therefore, R is symmetric.
Transitive:
Let (x, y) ∈ R, where x, y ∈ Z.
⇒ (x – y) is divisible by 5.
⇒ x – y = 5Afor some A ∈ Z Again, let (y, z) ∈ R, where y, z ∈ Z.
⇒ (y – 1) is divisible by 5.
⇒ y – z = 5B for some B ∈ Z.
Now, (x – y) + (y – 2) = 5A + 5B
⇒ x – z = 5(A + B)
⇒ (x – z) is divisible by 5 for some (A + B) ∈ Z
⇒ (x, z) ∈ R
Therefore, R is transitive.
Thus, R is reflexive, symmetric and transitive. Hence, it is an equivalence relation.
Note: If atleast one of the conditions, i.e. reflexive, symmetric and transitive, is not satisfied, then we say that the given relation is not an equivalence relation.
Question 41.
Consider f: R+ → [-5, ∞) given by f(x) = 9x2 + 6x – 5. Show that f is invertible with f-1(y) = \(\left(\frac{\sqrt{y+6}-1}{3}\right)\). Hence find
(i) f-1(10)
(ii) y if -1(y) = \(\frac{4}{3}\)
where R+ is the set of all non-negative real numbers. (Delhi 2017; Foreign 2010)
Answer:
Here, function f: R+ → [-5, ∞) given by f(x) = 9x2 + 6x – 5
One-one function:
Let x1, x2 ∈ R+ such that
f(x1) = f(x2)
Then, 9x12 + 6x1 – 5 = 9x2 + 6x2 – 5
⇒ 9(x12 – x22) + 6(x1 – x2) = 0
⇒ 9(x1 + x2)(x1 – x2) + 6(x1 – x2) = 0
⇒ (x1 – x2)[9(x1 + x2) + 6] = 0
⇒ x1 – x2 = 0 [∵ x1, x2 ∈ R+ ∴ 9(x1 + x2 + 6 ≠ 0)
⇒ x1 = x2, ∀ x1, x2 ∈ R+
Therefore, f(x) is one-one function.
Onto function:
Let y be any arbitrary element of
Then, y = f(x)
y = 9x2 + 6x – 5
y = (3x + 1)2 – 1 – 5= (3x + 1)2 – 6
(3x + 1)2 = y + 6
3x + 1 = y/y + 6, as y ≥ -5 ⇒ y + 6 ≥ 0
x = \(\frac{\sqrt{y+6}-1}{3}\)
Therefore, f is onto, thereby range f = [- 5, ∞)
Let us define g:[-5, ∞) → R+ as g(y) = \(\frac{\sqrt{y+6}-1}{3}\)
Now, (gof)(x) = g[f(x)] = g(9x2 + 6x – 5)
= g(3x + 1)2 – 6)
![Relations and Functions Class 12 Maths Important Questions Chapter 1 19]()
= y + 6 – 6 = y
Therefore, gof = IR+ and fog = I[-5, ∞)
Hence, f is invertible and the inverse of f is given by
f-1(y) = g(y) = \(\frac{\sqrt{y+6}-1}{3}\)
(i) ∴ f-1(10) = \(\frac{\sqrt{10+6}-1}{3}=\frac{\sqrt{16}-1}{3}=\frac{4-1}{3}\) = 1
(ii) If f-1(y) = \(\frac{4}{3}\) ⇒ y = f(4/3) = 9(4/3)2 + 6(4/3) – 5
= 16 + 8 – 5 = 19
Question 42.
Consider f : R – \(\left\{-\frac{4}{3}\right\}\) → R – \(\left\{\frac{4}{3}\right\}\) given by f(x) = \(\frac{4 x+3}{3 x+4}\). Show that f is bijective. Find the inverse of f and hence find f-1(0) and x such that f-1(x) = 2. (All India 2017)
Answer:
Given, f: R – \(\left\{-\frac{4}{3}\right\}\) → R – \(\left\{\frac{4}{3}\right\}\)
defined as f(x) = \(\frac{4 x+3}{3 x+4}\)
Let x1, x2 ∈ R – \(\left\{-\frac{4}{3}\right\}\)
such that f(x1) = f(x2)
⇒ \(\frac{4 x_{1}+3}{3 x_{1}+4}=\frac{4 x_{2}+3}{3 x_{2}+4}\)
⇒ (4x1 + 3)(3x2 + 4) = (3x1 + 4)(4x2 + 3)
⇒ 12x1x2 + 16x1 + 9x2 + 12 = 12x1x2 + 9x1 + 16x2 + 12
⇒ 7x1 = 7x2 ⇒ x1 = x2 ⇒ f is one-one.
Let y ∈ R – \(\left\{-\frac{4}{3}\right\}\), such that y ≠ \(\frac{4}{3}\)
The function f is onto if there exist
x ∈ R – \(\left\{-\frac{4}{3}\right\}\), such that f(x) = y
Now, f(x) = y ⇒ \(\frac{4 x+3}{3 x+4}\) = y ⇒ 4x + 3 = y (3x + 4)
⇒ 4x + 3 = 3xy + 4y ⇒ 4x – 3xy = 4y – 3
⇒ x (4 – 3y) = 4y – 3
⇒ x = \(\frac{4 x+3}{3 x+4}\) ∈ R – \(\left\{-\frac{4}{3}\right\}\) (y ≠ \(\frac{4}{3}\))
Thus, for any y ∈ R – \(\left\{\frac{4}{3}\right\}\)
Since, f is one-one and onto, so f-1 exists
![Relations and Functions Class 12 Maths Important Questions Chapter 1 20]()
Question 43.
Let f: N → N be a function defined as f(x) – 9x2 + 6% – 5. Show that f: N → S, where S is the range of f, is invertible. Find the inverse of f and hence find f-1(43) and f-1(-3). (Delhi 2016)
Answer:
We have a mapping f: N → N given by
f(x) = 9x2 + 6x – 5
One-one function:
Let x1, x2 ∈ N. such that
f(x1) = f(x2)
Then, 9x12 + 6x1 – 5= 9x22 + 6x2 – 5
⇒ 9x12 + 6x1 = 9x22 + 6x2
⇒ 9(x12 – x22) + 6 (x1 – x2) = o
⇒ 3(x1 – x2)(x1 + x2) + 2(x1 – x2) = 0 [divide by 3]
⇒ (x1 – x2) (3x1 + 3x2 + 2) = 0
∴ x1 – x2 = 0 or 3x1 + 3x2 + 2 = 0
But 3x1 + 3x2 + 2 ≠ 0 [: x1, x2 ∈ N)
∴ x1 – x2 = 0 = x1 = x2
So, f is one-one function.
Onto function:
Obviously, f : N → S is an onto function, because S is the range of f.
Thus, f :N → S is one-one and onto function.
⇒ f is invertible function, so its inverse exists.
Let f(x) = y, then y = 9×2 + 6x – 5 (1)
⇒ y = (3x)2 + 2 – 3x – 1 + 1 – 6
⇒ y = (3x + 1)2 – 6
⇒ (3x + 1 )2 = y + 6
⇒ 3x + 1 = \(\sqrt{y+6}\) [taking positive square root as x ∈ N]
![Relations and Functions Class 12 Maths Important Questions Chapter 1 21]()
Question 44.
If f, g: R → R be two functions defined as f(x)= |x| + x and g(x)= |x| – x, ∀ x ∈ R. Then, find fog and gof. Hence find fog (-3), fog{ 5) and gof(-2). (Foreign 2016)
Answer:
(i) Given, f(x) = |x| + x and g(x) = |x| – x, ∀ x ∈ R.
![Relations and Functions Class 12 Maths Important Questions Chapter 1 8]()
Thus, for x ≥ 0,gof (x) = g(f(x)) = g(2x) = 0
and for x < 0, gof(x) = g(f(x)) = g(0) = 0 ⇒ gof(x) = 0, ∀ x ∈ R Similarly, for x > 0, fog (x) = f(g(x)) = f(0) = 0
and for x < 0, fog (x) = f(g(x)) = f(-2x)
= 2(-2x) = -4x
![Relations and Functions Class 12 Maths Important Questions Chapter 1 9]()
(ii) We have, gof(x) = 0, ∀ x ∈ R.
![Relations and Functions Class 12 Maths Important Questions Chapter 1 22]()
Clearly, fg(-3) = -4(-3) = 12,
fog(5) = 0 and gof(-2) = 0.
Question 45.
If N denotes the set of all natural numbers and R be the relation on N × N defined by (a, b) R (c, d), if ad(b + c) = bc(a + d). Show that R is an equivalence relation. (Delhi 2015)
Answer:
We have, a relation R on N × N defined by (a, b)R(c, d), if ad(b + c) = bc(a + d).
Reflexive:
Let (a, b) ∈ N × N be any arbitrary element. We have to show {a, b) R {a, b), i.e. to show ab(b + a) = ba(a + b) which is trivally true as natural numbers are commutative under usual multiplication and addition.
Since, (a, b) ∈ N × N was arbitrary, therefore R is reflexive.
Symmetric:
Let (a, b), (c, d) ∈ N × N such that (a, b) R (c, d), i.e. ad(b + c) = bc(a + d) …(i)
To show, (c, d) R (a, b), i.e. to show cb(d + a) = da(c + b)
From Eq.(i), we have
ad(b + c) = bc(a + d)
⇒ da(c + b) = cb(d + a) [∵ natural numbers are commutative under usual addition and multiplication]
⇒ cb(d + a) = da(c + b)
⇒ (c, d) R (a, b)
Thus, R is symmetric.
Transitive:
Let (a, b), (c, d) and (e, f) ∈ N × N such that (a, b) R (c, d) and (c, d) R (e, f).
Now, (a, b) R (c, d) ⇒ ad(b + c) = bc(a + d)
![Relations and Functions Class 12 Maths Important Questions Chapter 1 23]()
⇒ af(e + b) = be(f + a)
⇒ af(b + e) = be(a + f)
⇒ (a, b) R (e, f)
⇒ R is transitive.
Thus, R is reflexive, symmetric and transitive, hence R is an equivalence relation.
Question 46.
Consider f: R+ → [-9, ∞) given by f(x) = 5x2 + 6x – 9. Prove that f is invertible with f-1(y) = \(\left(\frac{\sqrt{54+5 y}-3}{5}\right)\) [where, R+ is the set of all non-negative real numbers.] (All India 2015)
Answer:
Here, function f: R+ → [-5, ∞) given by f(x) = 9x2 + 6x – 5
One-one function:
Let x1, x2 ∈ R+ such that
f(x1) = f(x2)
Then, 9x12 + 6x1 – 5 = 9x2 + 6x2 – 5
⇒ 9(x12 – x22) + 6(x1 – x2) = 0
⇒ 9(x1 + x2)(x1 – x2) + 6(x1 – x2) = 0
⇒ (x1 – x2)[9(x1 + x2) + 6] = 0
⇒ x1 – x2 = 0 [∵ x1, x2 ∈ R+ ∴ 9(x1 + x2 + 6 ≠ 0)
⇒ x1 = x2, ∀ x1, x2 ∈ R+
Therefore, f(x) is one-one function.
Onto function:
Let y be any arbitrary element of
Then, y = f(x)
y = 9x2 + 6x – 5
y = (3x + 1)2 – 1 – 5= (3x + 1)2 – 6
(3x + 1)2 = y + 6
3x + 1 = y/y + 6, as y ≥ -5 ⇒ y + 6 ≥ 0
x = \(\frac{\sqrt{y+6}-1}{3}\)
Therefore, f is onto, thereby range f = [- 5, ∞)
Let us define g:[-5, ∞) → R+ as g(y) = \(\frac{\sqrt{y+6}-1}{3}\)
Now, (gof)(x) = g[f(x)] = g(9x2 + 6x – 5)
= g(3x + 1)2 – 6)
![Relations and Functions Class 12 Maths Important Questions Chapter 1 19]()
= y + 6 – 6 = y
Therefore, gof = IR+ and fog = I[-5, ∞)
Hence, f is invertible and the inverse of f is given by
f-1(y) = g(y) = \(\frac{\sqrt{y+6}-1}{3}\)
(i) ∴ f-1(10) = \(\frac{\sqrt{10+6}-1}{3}=\frac{\sqrt{16}-1}{3}=\frac{4-1}{3}\) = 1
(ii) If f-1(y) = \(\frac{4}{3}\) ⇒ y = f(4/3) = 9(4/3)2 + 6(4/3) – 5
= 16 + 8 – 5 = 19
Question 47.
Let f: N → R be a function defined as f(x) = 4x2 + 12x + 15.Show that f:N → S, where S is the range of f, is invertible. Also, find the inverse of f. (Foreign 2015)
Answer:
f-1(x) = \(\frac{\sqrt{x-6}-3}{2}\)
Question 48.
Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b): |a – b| is divisible by 2}, is an equivalence relation. Write all the equivalence classes of R. (All India 2015C)
Answer:
(i) Given relation is S = {(a, b): |a – b| is divisible by 4 and a, b ∈ A}
and A = {x : x ∈ Z and 0 ≤ x ≤ 12}
Now, A can be written as
A = {0,1, 2, 3, …,12}
Reflexive:
As for any x ∈ A, we get |x – x| = 0, which is divisible by 4.
⇒ (x, x) ∈ S, ∀ x ∈ A
Therefore, S is reflexive.
Symmetric:
As for any (x, y) ∈ S, we get |x – y| is divisible by 4. [by using definition of given relation]
⇒ |x – y| = 4λ, for some λ ∈ Z
⇒|y- x| = 4λ, for some λ ∈ Z
⇒ (y, x) ∈ S
Thus, (x, y) ∈ S ⇒ (y, x) ∈ S, ∀ x, y ∈ A
Therefore, S is symmetric.
Transitive:
For any (x, y) ∈ S and (y, z) ∈ S, we get |x – y| is divisible by 4 and |y – z| is divisible by 4. [by using definition of given relation]
⇒ |x – y| = 4λ and |y – z| = 4μ, for some λ, μ ∈ Z.
Now, x – z = (x – y) + (y – z)
= ± 4λ + 4μ
= ± 4 (λ, + μ)
⇒ |x – z| is divisible by 4.
⇒ (x, z) ∈ S
Thus, (x, y) ∈ S and (y, z) ∈ S
⇒ (x, z) ∈ S, ∀ x, y, z ∈ A
Therefore, S is transitive.
Since, S is reflexive, symmetric and transitive, so it is an equivalence relation. Now, set of all elements related to 1 is {1,5,9}.
(ii) Clearly, [1] = {1, 3, 5}
[2] = {2, 4}
[3] = {1, 3, 5} [4] = {2, 4}
and [5] = {1, 3, 5}
Thus, [1 ] = [3] = [5] = {1, 3, 5} and [2] = [4] = {2,4}
The post Relations and Functions Class 12 Maths Important Questions Chapter 1 appeared first on Learn CBSE.



































































































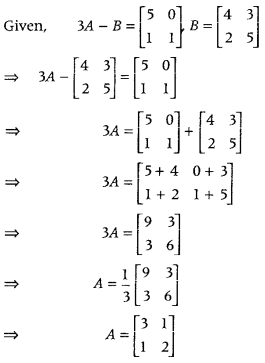
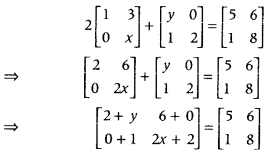
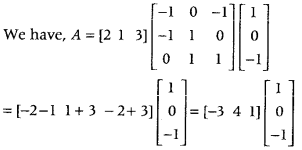
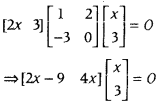
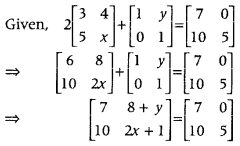







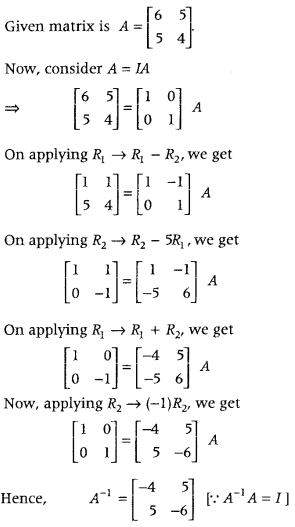
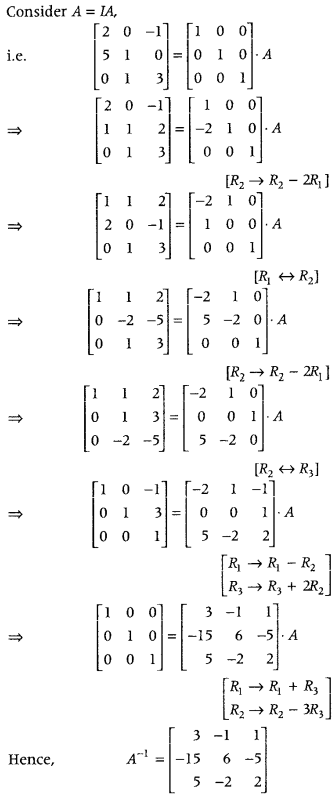
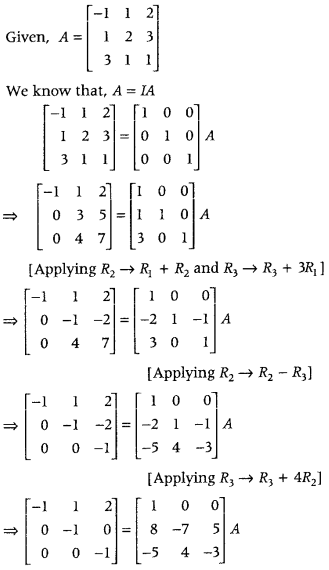
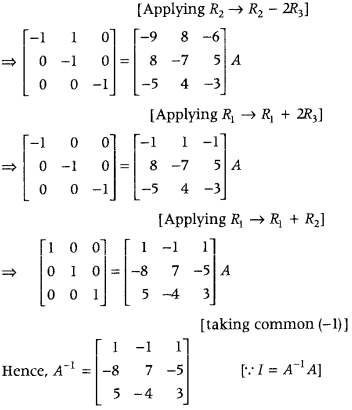
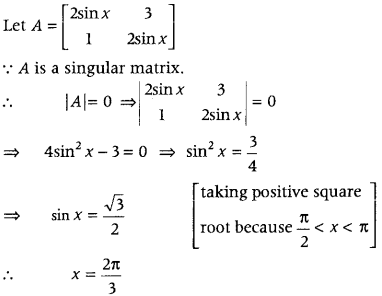
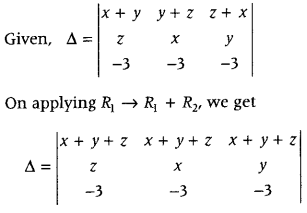

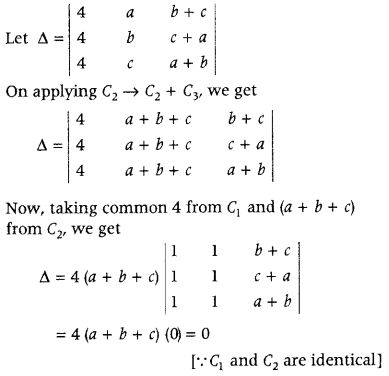
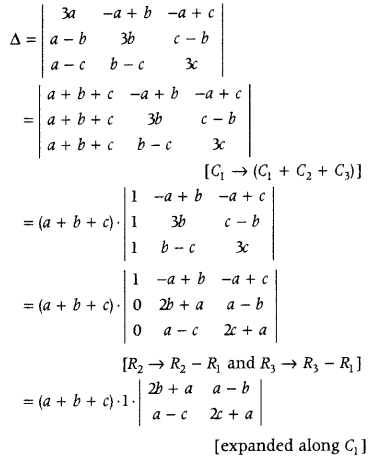









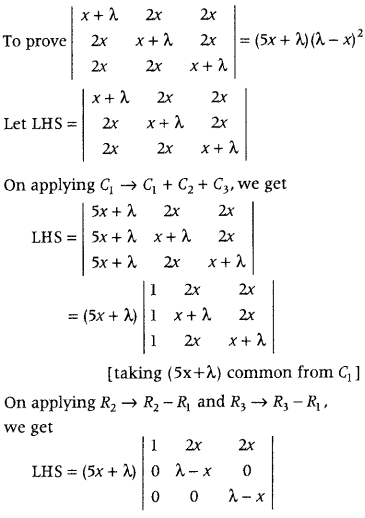

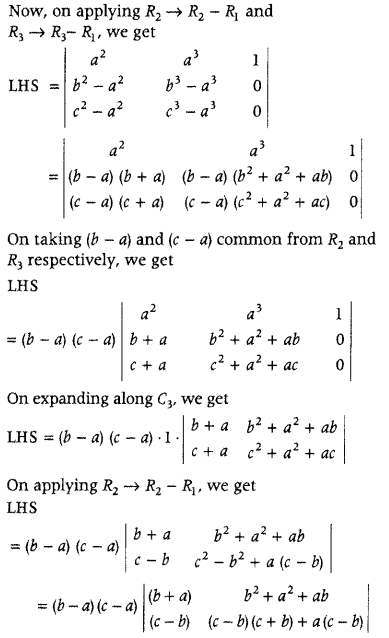




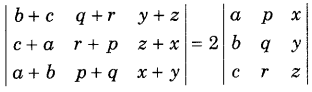
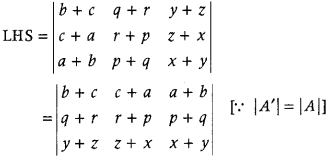




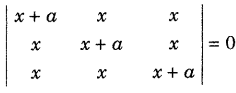
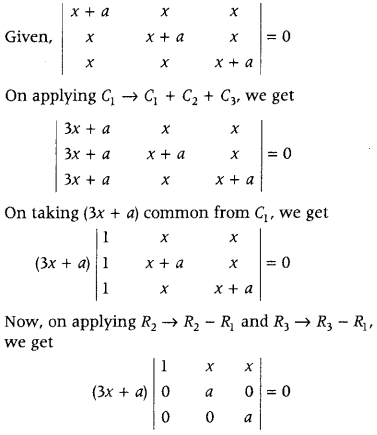
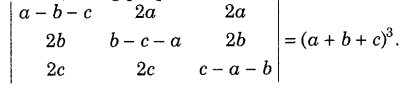
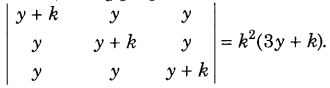
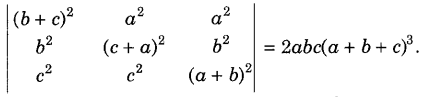

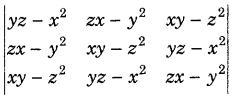

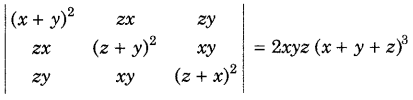
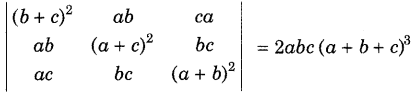

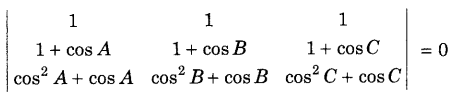
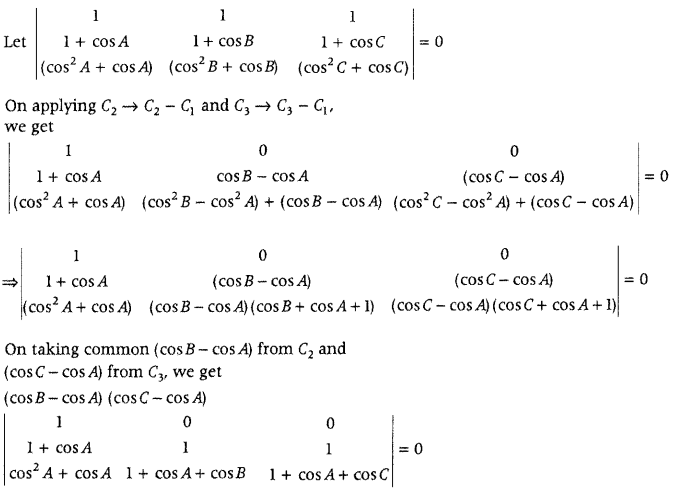
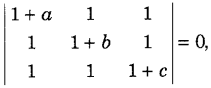

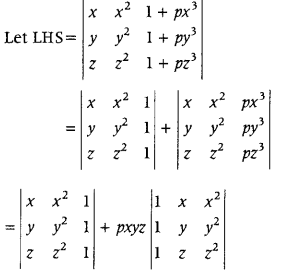


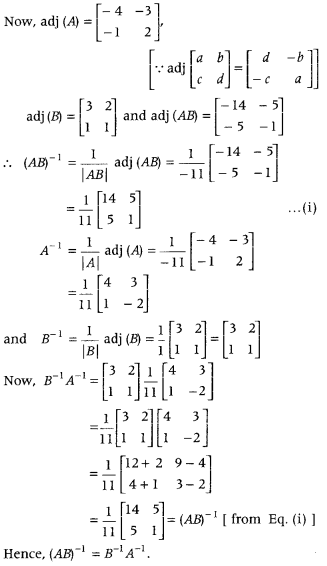

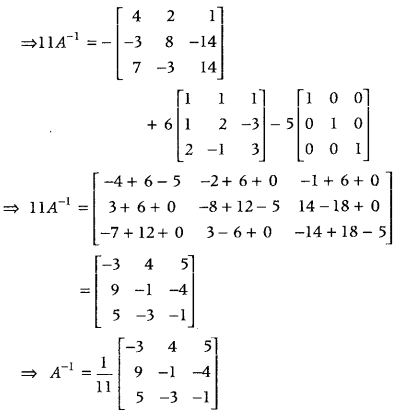
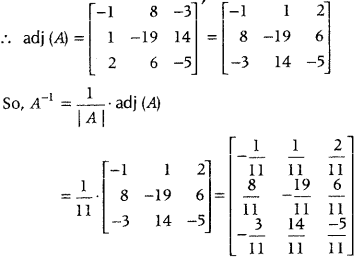
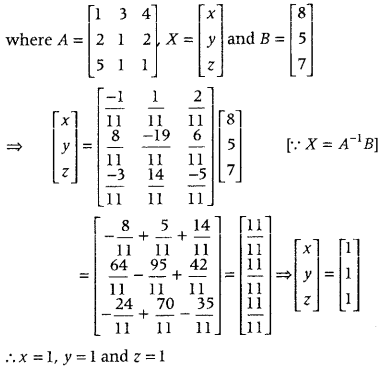
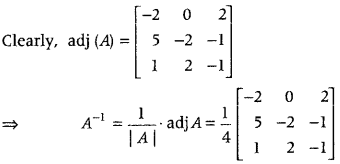
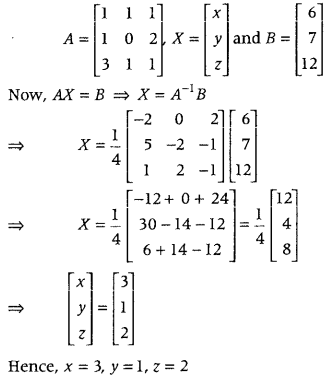
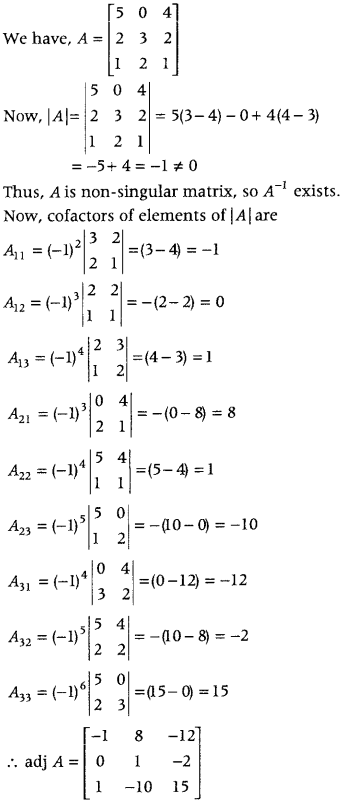
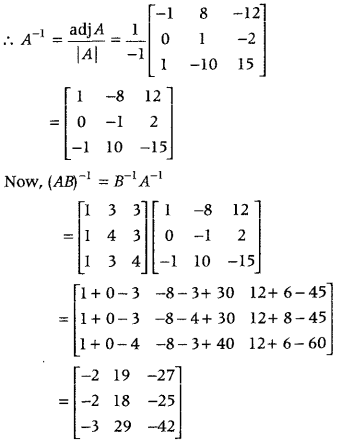
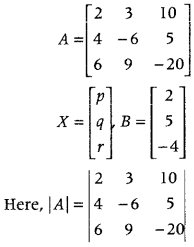
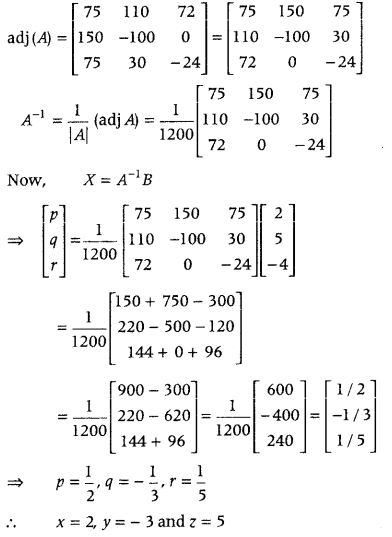
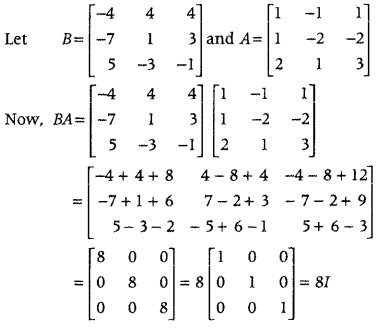
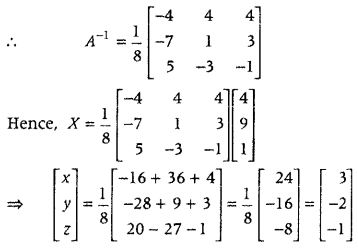

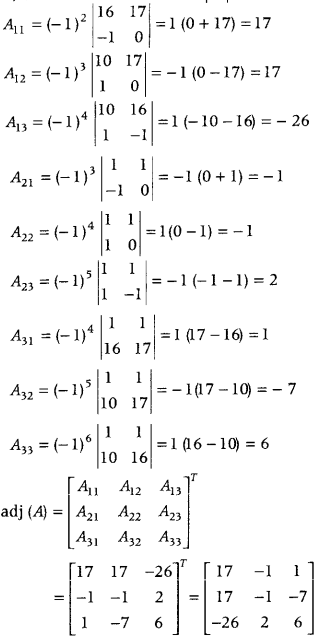

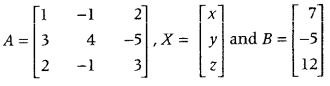
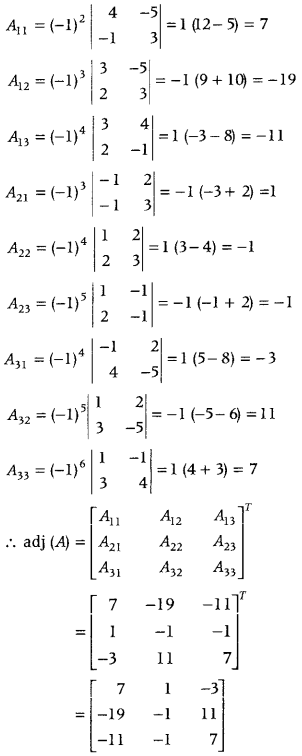
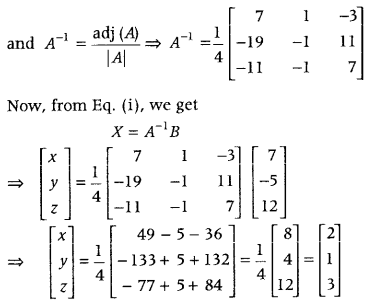
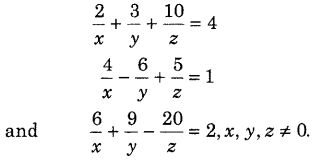
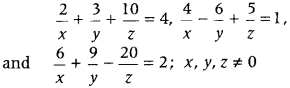
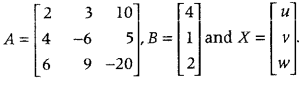
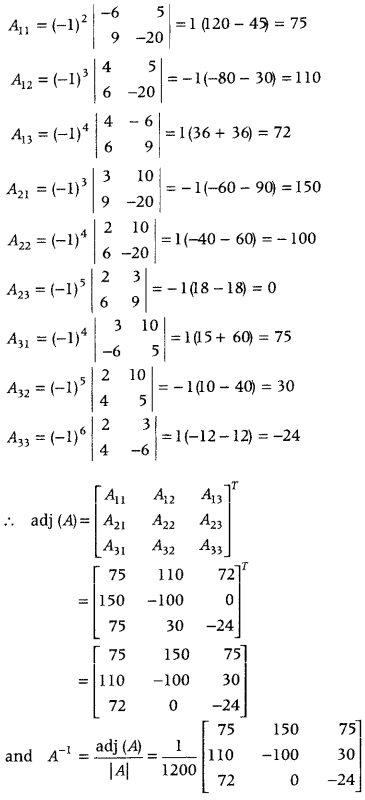
























 .
.